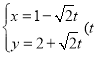Question

【题目】已知（）的方格表中的每个元素都是绝对值不大于1的实数，且方格表中所有元素之和等于0，试求最小的非负实数，使得每个这样的方格表中必有一行或一列，其元素之和的绝对值不大于．

Answer 1

【答案】

【解析】

首先，考虑方格表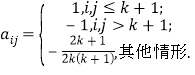

该方格表中前行，前列中元素之和均等于，

后行，后列中的元素之和的绝对值均等于．

因此，．

另一方面，设一方格表满足题设条件，且每行、每列之和的绝对值都大于．

不妨设前行每行元素之和都大于．

于是，前行的总和大于．

但子表的每列元素之和的绝对值都不大于，

故必有列每列元素之和为正，其所在的原方格表的列元素之和也是正的．

不妨设前列每列元素之和为正（从而大于）．

再注意到左上角的方块和右下角的方块中元素之和的绝对值分别不大于和，最后得到方格表元素之和大于

，矛盾．

综上，所求最小的非负实数．