题目内容
【题目】已知![]() ,
, ![]() ,函数
,函数![]() .
.
(1)求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(2)若![]() ,
, ![]() ,求
,求![]() 的值;
的值;
(3)若函数![]() 在区间
在区间![]() 上是单调递增函数,求正数
上是单调递增函数,求正数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
, ![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)利用数量积的计算得到![]() ,再利用二倍角公式和辅助角公式得到
,再利用二倍角公式和辅助角公式得到![]() ,从而可求
,从而可求![]() 在
在![]() 上的最值.(2)
上的最值.(2)![]() 等价于
等价于![]() ,把
,把![]() 变形为
变形为![]() ,利用两角差的余弦可以得到
,利用两角差的余弦可以得到![]() .(3)先求出
.(3)先求出![]() 单调增区间为
单调增区间为![]() ,因此存在
,因此存在![]() ,使得
,使得![]() ,从而
,从而![]() ,根据不等式的形式和
,根据不等式的形式和![]() 可得
可得![]() ,因此
,因此![]() .
.
解析:(1)![]()
![]() , 因为
, 因为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(2)因为![]() ,所以
,所以![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() ,所以
,所以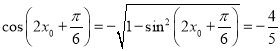 , 所以
, 所以![]()
![]() .
.
(3)![]() ,令
,令![]() 得
得![]() ,因为函数
,因为函数![]() 在
在![]() 上是单调递增函数, 所以存在
上是单调递增函数, 所以存在![]() ,使得
,使得![]() ,所以有
,所以有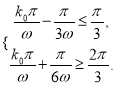 即
即![]() ,因为
,因为![]() 所以
所以![]() 又因为
又因为![]() , 所以
, 所以![]() , 所以
, 所以![]() 从而有
从而有![]() ,所以
,所以![]() ,所以
,所以![]()
(另解:由![]() ,得
,得![]() .因为
.因为![]() ,所以
,所以![]() ,所以
,所以![]() 或
或![]() ,解得
,解得![]() 或
或![]() .又
.又![]() ,所以
,所以![]() )
)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为迎接党的“十九大”胜利召开与响应国家交给的“提速降费”任务,某市移动公司欲提供新的资费套餐(资费包含手机月租费、手机拨打电话费与家庭宽带上网费)。其中一组套餐变更如下:
原方案资费
手机月租费 | 手机拨打电话 | 家庭宽带上网费(50M) |
18元/月 | 0.2元/分钟 | 50元/月 |
新方案资费
手机月租费 | 手机拨打电话 | 家庭宽带上网费(50M) |
58元/月 | 前100分钟免费, 超过部分 | 免费 |
(1)客户甲(只有一个手机号和一个家庭宽带上网号)欲从原方案改成新方案,设其每月手机通话时间为![]() 分钟(
分钟(![]() ),费用
),费用![]() 原方案每月资费-新方案每月资费,写出
原方案每月资费-新方案每月资费,写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)经过统计,移动公司发现,选这组套餐的客户平均月通话时间![]() 分钟,为能起到降费作用,求
分钟,为能起到降费作用,求![]() 的取值范围。
的取值范围。