题目内容
【题目】如图,在四面体P﹣ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC= ![]() .
. 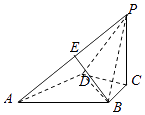
(1)求证:PA⊥BD;
(2)已知E是PA上一点,且BE∥平面PCD.若PC=2,求点E到平面ABCD的距离.
【答案】
(1)证明:连接AC交BD于O,
∵PC⊥BP,BP∩CP=P,
∴PC⊥AB,
∵AB⊥BP,BP∩CP=P,
∴AB⊥平面PBC,
∴AB⊥BC,
∵BC= ![]() ,
,
∴tan∠BAC= ![]() ,即∠BAC=30°,
,即∠BAC=30°,
∵∠ABD=60°,
∴∠AOB=90°,
∴AC⊥BD,
∵PC⊥BD,
∴BD⊥平面ACP,
∵AP平面APC,
∴PA⊥BD
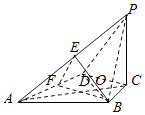
(2)解:取AD的中点F,连接BF,EF,
当E为PA的中点时,BE∥平面PCD,证明如下,
∵AB=BD,
∴BF⊥AD,
有(1)的BC=CD,则CD⊥AD,
∴EF∥CD,
∵E为PA的中点,
∴EF∥PD,
∴平面BEF∥平面PCD,
∵BE平面BEF,
∴BE∥平面PCD,
∵PC⊥底面ABCD,
∴点E到平面ABCD的距离等于 ![]() PC=1
PC=1
【解析】(1)连接AC交BD于O,利用线线垂直得到线面垂直,即可证明PA⊥BD;(2)当E为PA的中点时,BE∥平面PCD,并证明,并得到点E到平面ABCD的距离等于 ![]() PC,问题得以解决.
PC,问题得以解决.
【考点精析】本题主要考查了空间中直线与直线之间的位置关系的相关知识点,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能正确解答此题.

练习册系列答案
相关题目