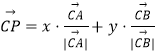Question

【题目】关于x的方程x3﹣ax+2=0有三个不同实数解，则实数a的取值范围是（ ）
A.（2，+∞）
B.（3，+∞）
C.（0，3 ）
D.（﹣∞，3）

Answer 1

【答案】B
【解析】解：令f（x）=x3﹣ax+2，则f′（x）=3x2﹣a，

若a≤0，则f′（x）≥0，∴f（x）为增函数，

∴f（x）最多只有1个零点，不符合题意；

若a＞0，令f′（x）=0得x=± ．

∴当x＜﹣ 或x＞ 时，f′（x）＞0，

当﹣ ＜x＜ 时，f′（x）＜0，

∴f（x）在（﹣∞，﹣ ）上单调递增，在（﹣ ， ）上单调递减，在（ ，+∞）上单调递增，

∴当x=﹣ 时，f（x）取得极大值f（﹣ ）= +2，

当x= 时，f（x）取得极小值f（ ）=﹣ +2，

∵f（x）有三个零点，

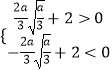∴ ，解得a＞3．

综上，a＞3．

故选B．