题目内容
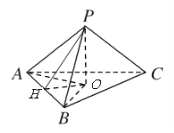
【题目】如图所示,在△ABC中,a=b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边,在四面体PABC中,S1,S2,S3,S分别表示△PAB,△PBC,△PCA,△ABC的面积,α,β,γ依次表示面PAB,面PBC,面PCA与底面ABC所成二面角的大小.写出对四面体性质的猜想,并证明你的结论


【答案】S=S1·cos α+S2·cos β+S3·cos γ
【解析】类比三角形中的结论,猜想在四面体中的结论为S=S1·cos α+S2·cos β+S3·cos γ.
证明:如图,设![]() 点在底面的射影为
点在底面的射影为![]() 点,过
点,过![]() 点作
点作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,
,
![]() 就是平面PAB与底面ABC所成的二面角,则
就是平面PAB与底面ABC所成的二面角,则![]() ,
,
![]() ,
,![]()
![]() 同理,
同理,![]() ,
,
又![]() ,
,![]() S=S1·cos α+S2·cos β+S3·cos γ.
S=S1·cos α+S2·cos β+S3·cos γ.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

