题目内容
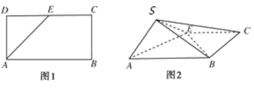
【题目】如图,已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,左准线
,左准线![]() :
:![]() 和右准线
和右准线![]() :
:![]() 分别与
分别与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 恰好为线段
恰好为线段![]() 的三等分点.
的三等分点.
(1)求椭圆![]() 的离心率;
的离心率;
(2)过点![]() 作直线
作直线![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点,且满足
两点,且满足![]() ,当△
,当△![]() 的面积最大时(
的面积最大时(![]() 为坐标原点),求椭圆
为坐标原点),求椭圆![]() 的标准方程.
的标准方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)根据![]() 、
、![]() 恰好为线段
恰好为线段![]() 的三等分点,得
的三等分点,得![]() ,即
,即![]() ,解得离心率(2)根据离心率可设椭圆方程为
,解得离心率(2)根据离心率可设椭圆方程为![]() .利用OD为定值表示三角形面积
.利用OD为定值表示三角形面积![]() ,联立直线方程
,联立直线方程![]() 与椭圆方程,结合韦达定理表示面积
与椭圆方程,结合韦达定理表示面积![]() ,分离利用基本不等式求最值,确定
,分离利用基本不等式求最值,确定![]() ,最后根据
,最后根据![]() 得
得![]() ,求出
,求出![]() ,解出
,解出![]()
试题解析:(1)焦点![]() ,右准线
,右准线![]() :
:![]() ,由题知
,由题知![]() ,
,
即![]() ,即
,即![]() ,解得
,解得![]() .
.
(2)由(1)知![]() ,得
,得![]() ,
,![]() ,可设椭圆方程为
,可设椭圆方程为![]() .
.
设直线![]() 的方程为
的方程为![]() ,代入椭圆的方程有,
,代入椭圆的方程有,![]() ,
,
因为直线与椭圆相交,所以![]() ,
,
由韦达定理得![]() ,
,![]() ,又
,又![]() ,所以
,所以![]() ,
,
得到![]() ,
,![]() ,
,![]() ,得到
,得到![]() ,
,
所以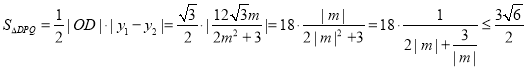 ,
,
当且仅当![]() 时,等号成立,此时
时,等号成立,此时![]() ,代入
,代入![]() 满足
满足![]() w,
w,
所以所求椭圆方程为![]() .
.

练习册系列答案
相关题目
【题目】在一次篮球定点投篮训练中,规定每人最多投3次.在![]() 处每投进一球得3分;在
处每投进一球得3分;在![]() 处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次. 某同学在
处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次. 某同学在![]() 处的投中率
处的投中率![]() ,在
,在![]() 处的投中率为
处的投中率为![]() .该同学选择先在
.该同学选择先在![]() 处投一球,以后都在
处投一球,以后都在![]() 处投,且每次投篮都互不影响.用
处投,且每次投篮都互不影响.用![]() 表示
表示
该同学投篮训练结束后所得的总分,其分布列为:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的数学期望
的数学期望![]() ;
;
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在![]() 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小.