题目内容

13．已知${a_n}=\frac{1}{n-50.5}$（n∈N*），数列{an}的前项和为Sn，则使Sn＞0的n最小值是（　　）
A．99B．100C．101D．102

分析 通过${a_n}=\frac{1}{n-50.5}$可得ai+a101-i=0（i∈N*），结合a101＞0即得结论．

解答 解：∵${a_n}=\frac{1}{n-50.5}$=$\frac{2}{2n-101}$（n∈N*），
∴ai+a101-i=0（i∈N*），
∴a1+a100=a2+a99=…=a45+a46=0，a101＞0，
又∵S99＜0，S100=0，S101＞0，
∴使Sn＞0的n的最小值为101，
故选：C．

点评 本题考查求数列的和，注意解题方法的积累，属于中档题．

练习册系列答案
相关题目
9．已知cosθ＞0，tanθ＜0，则$\sqrt{1-co{s}^{2}θ}$化简结果为（　　）
A．±sinθB．sinθC．-sinθD．以上都不对
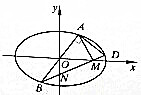10．函数y=tan（2x+$\frac{π}{3}$）的递增区间是（$\frac{kπ}{2}$-$\frac{5π}{12}$，$\frac{kπ}{2}$+$\frac{π}{12}$ ），k∈z．
1．不等式$lo{g_{\frac{1}{5}}}（{x^2}-2x-3）＞{x^2}$-2x-9的解集为（-2，-1）∪（3，4）．
8．对于椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），c为椭圆半焦距，e为椭圆离心率，过原点O的直线与椭圆C交于A、B两点（A、B不是椭圆C的顶点），点D在椭圆C上，且AD⊥AB，直线BD与x轴、y轴分别交于M、N两点，证明：
（1）当e≠$\frac{\sqrt{2}}{2}$时，设直线BD、AM的斜率分别为k1、k2，则k1=（1-2e2）k2，当e=$\frac{\sqrt{2}}{2}$时，则直线AM与x轴垂直；
（2）△OMN面积的最大值为$\frac{{c}^{4}}{4ab}$．
18．将函数y=sin（2x+φ）的图象沿x轴向左平移$\frac{π}{8}$个单位后，得到一个偶函数的图象，则φ的取值为φ=kπ+$\frac{π}{4}$，k∈z．
5．圆锥底面半径为3，母线长为12，B是母线PA的中点，则点A绕圆锥一周到达点B的最短距离为$6\sqrt{5}$．
2．已知a，b均为实数，logb（3a-1）为正数，点（b，a）在圆（x-$\frac{1}{2}$）2+（y+$\frac{1}{3}$）2=c2上，其中c＞0，则c的取值范围是（$\frac{2}{3}$，$\frac{\sqrt{5}}{2}$）∪（$\frac{\sqrt{5}}{2}$，+∞）．
3．设复数z满足z（2-3i）=6+4i（其中i为虚数单位），则z的模为2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网