题目内容
16. 从某体校学生中选出男生14人,女生6人测量身高,被测学生身高的茎叶图如图所示(单位:cm),现规定,身高在180cm以上的参加校篮球队,180cm以下的参加田径队.
从某体校学生中选出男生14人,女生6人测量身高,被测学生身高的茎叶图如图所示(单位:cm),现规定,身高在180cm以上的参加校篮球队,180cm以下的参加田径队.(I)求女生身高的平均值;
(Ⅱ)①先采用分层抽样的方式分别从篮球队和田径队中选出5人参了加某项活动.篮球队和田径队分别选出多少人?②若从这5人中随机选2人,那么至少1人选自篮球队的概率是多少?
分析 (Ⅰ)由茎叶图,能求出女生身高的平均值.
(Ⅱ)①篮球队有8人,田径队有12人,由此采用分层抽样的方式能求出从篮球队和田径队分别选出多少人.
②从从这5人中随机选2人,先求出基本事件总数,再求出2人至少1人选自篮球队包含的基本事件个数,由此能求出至少1人选自篮球队的概率.
解答 解:(Ⅰ)由茎叶图,得女生身高的平均值:
$\overline{x}$=$\frac{168+177+178+185+186+192}{6}$=181cm.
(Ⅱ)①篮球队有8人,田径队有12人,
∴8×$\frac{5}{20}$=2人,$12×\frac{5}{20}$=3人,
∴采用分层抽样的方式从篮球队和田径队分别选出2人和3人.
②从从这5人中随机选2人,基本事件总数n=${C}_{5}^{2}$=10,
2人至少1人选自篮球队包含的基本事件个数m=${C}_{5}^{2}-{C}_{3}^{2}$=7,
∴至少1人选自篮球队的概率p=$\frac{m}{n}$=$\frac{7}{10}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意茎叶图、分层抽样、等可能事件概率计算公式的合理运用.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
7.已知数列{an}满足a1=1,an+1-an=2,等比数列{bn}满足b1=a1,b4=a4+1.
(1)求数列{an},{bn}的通项公式;
(2)设cn=an•bn,求数列{cn}的前n项和Sn.
(1)求数列{an},{bn}的通项公式;
(2)设cn=an•bn,求数列{cn}的前n项和Sn.
1. 在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
(Ⅰ)完成频率分布表,并画出频率分布直方图;
(Ⅱ)从纤度最小、最大的6件产品中任取2件,设取出的纤度在[1.30,1.34)内的产品有ξ件,求ξ的分布列和期望.
 在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.| 分组 | 频数 | 频率 |
| [1.30,1.34) | 4 | |
| [1.34,1.38) | 25 | |
| [1.38,1.42) | 30 | |
| [1.42,1.46) | 29 | |
| [1.46,1.50) | 10 | |
| [1.50,1.54) | 2 | |
| 合计 | 100 |
(Ⅱ)从纤度最小、最大的6件产品中任取2件,设取出的纤度在[1.30,1.34)内的产品有ξ件,求ξ的分布列和期望.
5.下列关系中正确的个数为( )
①$\frac{1}{2}$∈R ②$\sqrt{2}$∉Q ③|-3|∉N+ ④|-$\sqrt{3}$|∈Q.
①$\frac{1}{2}$∈R ②$\sqrt{2}$∉Q ③|-3|∉N+ ④|-$\sqrt{3}$|∈Q.
| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
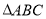 中,角
中,角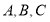 的对边分别是
的对边分别是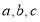 ,已知
,已知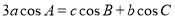 .
.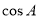 的值;
的值;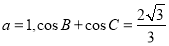 ,求边
,求边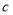 的值.
的值.