题目内容
7.已知数列{an}满足a1=1,an+1-an=2,等比数列{bn}满足b1=a1,b4=a4+1.(1)求数列{an},{bn}的通项公式;
(2)设cn=an•bn,求数列{cn}的前n项和Sn.
分析 (1)通过a1=1、an+1-an=2可知数列{an}是首项为1、公差为2的等差数列,进而计算即得结论;
(2)通过(1)可知cn=(2n-1)•2n-1,利用错位相减法计算即得结论.
解答 解:(1)∵a1=1,an+1-an=2,
∴an=1+2(n-1)=2n-1,
∴b1=a1=1,b4=a4+1=8,
∴公比q=$\root{3}{\frac{{b}_{4}}{{b}_{1}}}$=$\root{3}{\frac{8}{1}}$=2,
∴bn=2n-1;
(2)由(1)可知cn=an•bn=(2n-1)•2n-1,
∴Sn=1•20+3•21+…+(2n-1)•2n-1,
2Sn=1•21+3•22+…+(2n-3)•2n-1+(2n-1)•2n,
错位相减得:-Sn=1+2(21+22+…+2n-1)-(2n-1)•2n,
∴Sn=-1-2(21+22+…+2n-1)+(2n-1)•2n
=-1-2•$\frac{2(1-{2}^{n-1})}{1-2}$+(2n-1)•2n
=3+(2n-3)•2n.
点评 本题考查数列的通项及前n项和,考查错位相减法,注意解题方法的积累,属于中档题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
18.当a>0且a≠1时,函数f(x)=ax+1-1的图象一定过点( )
| A. | (0,1) | B. | (0,-1) | C. | (-1,0) | D. | (1,0) |
12.函数y=2x与y=log2x的图象( )
| A. | 关于x轴对称 | B. | 关于原点对称 | ||
| C. | 关于直线y=x对称 | D. | 关于直线y=-x对称 |
19.已知f′(x)是定义在R上的奇函数f(x)的导数,且2f(x)+xf′(x)>x2,则函数f(x)的零点的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 1个或2个 |
16.第三象限的角的集合可表示为( )
| A. | {α|90°<α<180°} | B. | {α|180°<α<270°} | ||
| C. | {α|90°+k•360°<α<180°+k•360°,k∈Z} | D. | {α|180°+k•360°<α<270°+k•360°,k∈Z} |
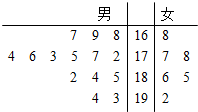 从某体校学生中选出男生14人,女生6人测量身高,被测学生身高的茎叶图如图所示(单位:cm),现规定,身高在180cm以上的参加校篮球队,180cm以下的参加田径队.
从某体校学生中选出男生14人,女生6人测量身高,被测学生身高的茎叶图如图所示(单位:cm),现规定,身高在180cm以上的参加校篮球队,180cm以下的参加田径队.