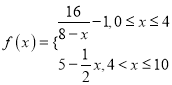题目内容
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,椭圆C与y轴交于A、B两点,|AB|=2.
,椭圆C与y轴交于A、B两点,|AB|=2.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点P是椭圆C上的动点,且直线PA,PB与直线x=4分别交于M、N两点,是否存在点P,使得以MN为直径的圆经过点(2,0)?若存在,求出点P的横坐标;若不存在,说明理由.
【答案】(Ⅰ)![]() (Ⅱ)P不存在
(Ⅱ)P不存在
【解析】
试题分析:(Ⅰ)运用椭圆的离心率公式,以及a,b,c的关系,计算即可得到所求椭圆方程;(Ⅱ)设P(m,n),可得![]() ,可得A(0,1),B(0,-1),设M(4,s),N(4,t),运用三点共线的条件:斜率相等,求得M,N的坐标,再由直径所对的圆周角为直角,运用垂直的条件:斜率之积为-1,计算即可求得m,检验即可判断是否存在
,可得A(0,1),B(0,-1),设M(4,s),N(4,t),运用三点共线的条件:斜率相等,求得M,N的坐标,再由直径所对的圆周角为直角,运用垂直的条件:斜率之积为-1,计算即可求得m,检验即可判断是否存在
试题解析:(Ⅰ)由题意可得e=![]()
![]() =
=![]() ,2b=2,即b=1,
,2b=2,即b=1,
又a2﹣c2=1,解得a=2,c=![]()
![]() ,
,
即有椭圆的方程为![]() +y2=1;
+y2=1;
(Ⅱ)设P(m,n),可得![]() +n2=1,
+n2=1,
即有n2=1﹣![]() ,
,
由题意可得A(0,1),B(0,﹣1),设M(4,s),N(4,t),
由P,A,M共线可得,kPA=kMA,即为![]() =
=![]() ,
,
可得s=1+![]() ,
,
由P,B,N共线可得,kPB=kNB,即为![]() =
=![]() ,
,
可得s=![]() ﹣1.
﹣1.
假设存在点P,使得以MN为直径的圆经过点Q(2,0).
可得QM⊥QN,即有![]()
![]()
![]()
![]() =﹣1,即st=﹣4.
=﹣1,即st=﹣4.
![]() ][
][![]() ﹣1]=﹣4,
﹣1]=﹣4,
化为﹣4m2=16n2﹣(4﹣m)2=16﹣4m2﹣(4﹣m)2,
解得m=0或8,
由P,A,B不重合,以及|m|<2,可得P不存在.

【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的.
开始计数的.
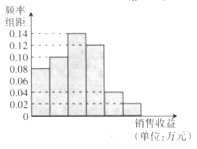
(Ⅰ)根据频率分布直方图计算图中各小长方形的宽度;
(Ⅱ)估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(Ⅲ)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
销售收益y(单位:万元) | 2 | 3 | 2 | 7 |
表中的数据显示,![]() 与
与![]() 之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算
之间存在线性相关关系,请将(Ⅱ)的结果填入空白栏,并计算![]() 关于
关于![]() 的回归方程.
的回归方程.
回归直线的斜率和截距的最小二乘估计公式分别为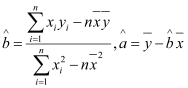 .
.