题目内容
【题目】市场上有一种新型的强力洗衣粉,特点是去污速度快,已知每投放![]() (
(![]() 且
且![]() )个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度
)个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为![]() ,其中
,其中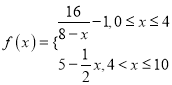 ,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
(1)若只投放一次4个单位的洗衣液,则有效去污时间可能达几分钟?
(2)若先投放2个单位的洗衣液,6分钟后投放![]() 个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求
个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求![]() 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: ![]() 取
取![]() ).
).
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)当![]() 时,代入
时,代入![]() ,依题意有效去污满足
,依题意有效去污满足![]() ,即
,即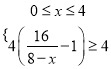 或
或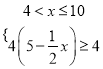 ,解得
,解得![]() ,故有效去污时间可能达
,故有效去污时间可能达![]() 分钟;(2)由于某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,故设项对应的浓度为
分钟;(2)由于某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,故设项对应的浓度为![]() ,此时
,此时![]() ,
, ![]() ,
, 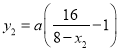 ,
, ![]() ,令
,令![]() ,将浓度相加,得
,将浓度相加,得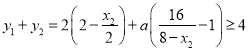 ,分离参数得
,分离参数得![]() ,利用换元法和基本不等式求得
,利用换元法和基本不等式求得![]() ,故
,故![]() 的最小值为
的最小值为![]() .
.
试题解析:
(1)由题意知有效去污满足![]() ,则
,则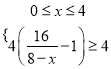 或
或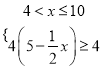
得![]() ,所以有效去污时间可能达8分钟.
,所以有效去污时间可能达8分钟.
(2)![]() ,
, ![]() ,
, 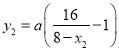 ,
, ![]()
令![]() ,
, 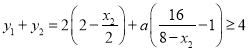 ,
, ![]()
∴![]() ,若令
,若令![]() ,
, ![]() ,
,
又![]() ,
,
所以![]() 的最小值为1.6.
的最小值为1.6.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(参考公式: 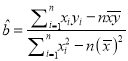 ,
, ![]() )
)