题目内容
【题目】定义在![]() 上的函数
上的函数![]() 的导函数为
的导函数为![]() ,且满足
,且满足![]() ,
, ![]() ,当
,当![]() 时有
时有![]() 恒成立,若非负实数
恒成立,若非负实数![]() 、
、![]() 满足
满足![]() ,
, ![]() ,则
,则![]() 的取值范围为 .
的取值范围为 .
【答案】![]()
【解析】试题分析:由y=f′(x)图象可知,当x=0时,f′(x)=0,
当x∈(-∞,0)时,f′(x)<0,f(x)单调递减,
当x∈(0,+∞)时,f′(x)>0,f(x)单调递增,
又∵a,b为非负实数,
∴f(2a+b)≤1可化为f(2a+b)≤1=f(3),可得0≤2a+b≤3,
同理可得-2≤-a-2b≤0,即0≤a+2b≤2,
作出以及a≥0和b≥0所对应的平面区域,
得到如图的阴影部分区域,
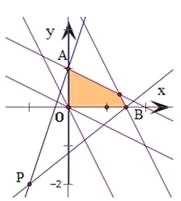
解之得A(0,1)和B(1.5,0)
而等于可行域内的点与P(-1,-2)连线的斜率,
结合图形可知:kPB是最小值,kPA是最大值,
由斜率公式可得:kPA=3,kPB=![]() ,
,
故![]() 的取值范围为
的取值范围为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目