题目内容

19．在△ABC中，若sinAcosB=1-cosAsinB，则△ABC为（　　）
A．锐角三角形B．直角三角形C．钝角三角形D．无法判定

分析 直接利用两角和的正弦函数化简求解，即可判断三角形的形状．

解答 解：在△ABC中，若，
可得sinAcosB+cosAsinB=1，
即sin（A+B）=1，
可得A+B=90°，∴C=90°，
三角形是直角三角形．
故选：B．

点评 本题考查两角和与差的三角函数，三角形的形状的判断，是基础题．

练习册系列答案
相关题目
9．△ABC中，sinB=sinAcosC，其中A、B、C是△ABC的三内角，则△ABC是直角三角形．
10．函数y=2sinx-1的最小值为（　　）
A．-3B．-2C．-1D．0
7．当实数m为何值时，复数z=（m2-2m-3）+（m2-1）i是：
（1）实数（2）虚数（3）纯虚数（4）实数0．
14．已知函数f（x）=$\frac{x}{4}$+$\frac{a}{x}$-lnx-$\frac{3}{2}$，其中a∈R，且曲线y=f（x在点（1，f（1））处的切线垂直于直线y=$\frac{1}{2}$x．
（1）求a的值及在点（1，f（1））处的切线方程；
（2）求函数f（x）的单调区间与极值．
4．在一个不透明的口袋里装有外观相同的白球和黑球共20个，某学习小组做摸球试验，试验方法如图所示，试验得到了一组统计数据（表1）

①请估计：当n很大时，摸到白球的频率将会接近0.60．
②假如你去摸一次球，你摸到白球的概率是0.6，摸到黑球的概率是0.4；
③口袋中白球的个数约为12，黑球的个数约为8．
表1：
n1001502005008001000
m5896116295484601
11．曲线y=x（3lnx+1）在点（1，1）处的切线方程为（　　）
A．y=-4x+3B．y=-4x-3C．y=4x+3D．y=4x-3
8．设数列{an}，{bn}均为正项数列，其中a1=2，b1=1，b2=3，且满足an，bn+1，an+1成等比数列，bn，an，bn+1成等差数列．
（Ⅰ）（1）证明数列{$\sqrt{{a}_{n}}$}是等差数列；
（2）求通项公式an，bn；
（Ⅱ）设x${\;}_{n}=\frac{1}{（n+2）{a}_{n}}$，数列{xn}的前n项和记为Sn，证明：Sn$＜\frac{1}{2}$．
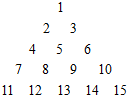9．把自然数1，2，3，4，…按如图方法排成一个数阵，根据如图排列规律，求数列中第n（n≥3）行从左到右的第三个数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网