题目内容
16.请你指出函数y=f(x)=$\frac{x}{1+|x|}$(x∈R)的基本性质(不必证明,并判断以下四个命题的正确性,必要时可直接运用有关其基本性质的结论加以证明)(1)当x∈R时,等式f(x)+f(-x)=0恒成立;
(2)若f(x1)≠f(x2),则一定有x1≠x2;
(3)若m>0,方程|f(x)|=m有两个不相等的实数解;
(4)函数g(x)=f(x)-x在R上有三个零点.
分析 运用绝对值的定义,将函数写成分段函数的形式,写出定义域和值域、奇偶性和单调性,运用奇偶性即可判断(1);
运用单调性即可判断(2);
运用数形结合的思想方法,画出y=|f(x)|和y=m的图象,观察即可得到m的范围,即可判断(3);
由函数方程的思想,可得f(x)=x只有一解,即可判断(4).
解答 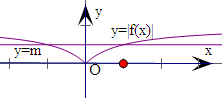 解:函数y=f(x)=$\frac{x}{1+|x|}$=$\left\{\begin{array}{l}{\frac{x}{1+x},x>0}\\{0,x=0}\\{\frac{x}{1-x},x<0}\end{array}\right.$,
解:函数y=f(x)=$\frac{x}{1+|x|}$=$\left\{\begin{array}{l}{\frac{x}{1+x},x>0}\\{0,x=0}\\{\frac{x}{1-x},x<0}\end{array}\right.$,
定义域为R,值域为(-1,1),函数f(x)为奇函数,
函数f(x)在(-∞,+∞)上递增.
对于(1),由f(x)为奇函数,可知(1)正确;
对于(2),由函数f(x)在(-∞,+∞)上递增,可知(2)正确;
对于(3),作出y=|f(x)|和y=m的图象,由图象观察可得
当0<m<1时,图象有两个交点,方程|f(x)|=m有两个不相等的实数解.
可知(3)错误;
对于(4),令g(x)=f(x)-x=0,即为f(x)=x,
当x=0时,f(0)=0成立;当x>0时,$\frac{x}{1+x}$=x,方程无解;
当x<0时,$\frac{x}{1-x}$=x,方程无解.即有函数g(x)只有一个零点.
可知(4)错误.
综上可得(1)(2)正确,(3)(4)错误.
点评 本题考查函数的性质和运用,主要考查绝对值函数的图象和性质,以及函数和方程的关系及转化思想,数形结合的思想方法,属于中档题和易错题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
7.已知点P在抛物线x2=4y上,那么点P到点M(-1,2)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
| A. | $(1,\frac{1}{4})$ | B. | $(-1,\frac{1}{4})$ | C. | (-1,2) | D. | (1,2) |
7.从抛物线y2=4x上一点P引抛物线准线的垂线,垂足为M,且|PM|=5,设抛物线的焦点为F,则△PMF的面积为( )
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
4.设复数z=1+ai(a是正实数),且|z|=$\sqrt{10}$,则$\frac{z}{1-2i}$等于( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
11.设复数z=1+ai(a是正实数),且$|z|=\sqrt{5}$,则z(1+i)等于( )
| A. | -1+3i | B. | 1-3i | C. | 1+3i | D. | -3+i |
1.若a<0,则下列不等式成立的是( )
| A. | $2a>{({\frac{1}{2}})^a}>{({0.2})^a}$ | B. | ${({\frac{1}{2}})^a}>{({0.2})^a}>2a$ | C. | ${({0.2})^a}>{({\frac{1}{2}})^a}>2a$ | D. | $2a>{({0.2})^a}>{({\frac{1}{2}})^a}$ |
5.i为虚数单位,复数$\frac{2i}{1+i}$的实部为 ( )
| A. | 1 | B. | -2 | C. | 2 | D. | -1 |
6.已知变量x,y满足:$\left\{\begin{array}{l}{2x-y≤0}\\{x-2y+3≥0}\\{x≥0}\end{array}\right.$,则z=($\sqrt{2}$)2x+y的最大值为( )
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 4 |