题目内容
8.求函数$y={sin^2}x+cosx+1,x∈[-\frac{π}{2},\frac{π}{2}]$的最大、小值,及取得最大、小值时x的取值集合.分析 问题可化为y=-t2+t+2(0≤t≤1)的最值,由二次函数区间的最值可得.
解答 解:由题意可得y=1-cos2x+cosx+1=-cos2x+cosx+2,
∵$x∈[-\frac{π}{2},\frac{π}{2}]$,∴0≤cosx≤1,
设t=cosx,则y=-t2+t+2(0≤t≤1)
∵关于t的二次函数开口向下,对称轴$t=-\frac{1}{2×(-1)}=\frac{1}{2}$,
∴函数y=-t2+t+2在$[0,\frac{1}{2}]$上为增函数,在$(\frac{1}{2},1]$上为减函数,
∴当$t=\frac{1}{2}$时,${y_{max}}=-\frac{1}{4}+\frac{1}{2}+2=2+\frac{1}{4}=\frac{9}{4}$,
此时$cosx=\frac{1}{2}$,$x=\frac{π}{3}$或$-\frac{π}{3}$,集合为$\left\{{\frac{π}{3},-\frac{π}{3}}\right\}$;
当t=1或t=0时,ymin=2,时cosx=0或cosx=1
此时$x=\frac{π}{2}$或$-\frac{π}{2}$或x=0,集合为$\left\{{\frac{π}{2},-\frac{π}{2},0}\right\}$
点评 本题考查三角函数的最值,换元并转化为二次函数区间的最值是解决问题的关键,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.各项都是正数的等比数列{an},若a2,$\frac{1}{2}$a3,2a1成等差数列,则$\frac{{a}_{3}+{a}_{4}}{{a}_{4}+{a}_{5}}$的值为( )
| A. | 2 | B. | 2或-1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{2}$或-1 |
3.某农副产品从5月1日起开始上市,通过市场调查,得到该农副产品种植成本Q(单位:元/kg)与上市时间t(单位:天)的数据如表:
(1)根据上表数据,从下列函数模型中选出一个适当的函数来描述农副产品种植成本Q与上市时间t的变化关系,要求简述你选择的理由并求出该函数表达式.参考函数:Q=at+b,Q=at2+bt+c;Q=abt;Q=alogbt(以上均有a≠0)
(2)利用你选出的函数模型,求该农副产品最低种植成本及相应的上市时间.
| 时间天 | 50 | 110 | 250 |
| 种植成本 | 150 | 108 | 150 |
(2)利用你选出的函数模型,求该农副产品最低种植成本及相应的上市时间.
20.已知$\overrightarrow a=(m+1,0,2m),\overrightarrow b=(6,2n-1,2),若\overrightarrow a∥\overrightarrow b$,则m与n的值分别为( )
| A. | $\frac{1}{5}$,$\frac{1}{2}$ | B. | -$\frac{1}{5}$,-$\frac{1}{2}$ | C. | 5,2 | D. | -5,-2 |
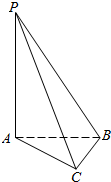 如图,在Rt△ABC中,AC=BC,PA⊥平面ABC,PB与平面ABC成60°角
如图,在Rt△ABC中,AC=BC,PA⊥平面ABC,PB与平面ABC成60°角