题目内容
6.若全称命题p:“对?x∈(1,3),x2-2ax-1≤0”为真命题,求实数a的取值范围.分析 令f(x)=x2-2ax-1,若全称命题p:“对?x∈(1,3),x2-2ax-1≤0”为真命题,则$\left\{\begin{array}{l}f(1)≤0\\ f(3)≤0\end{array}\right.$,解得答案.
解答 解:令f(x)=x2-2ax-1,
若全称命题p:“对?x∈(1,3),x2-2ax-1≤0”为真命题,
则$\left\{\begin{array}{l}f(1)≤0\\ f(3)≤0\end{array}\right.$,即$\left\{\begin{array}{l}-2a≤0\\ 8-6a≤0\end{array}\right.$,
解得:a≥$\frac{4}{3}$
点评 本题以全称命题为载体,考查了二次函数的性质,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的底面边长为$\sqrt{6}$时,其高的值为( )
| A. | 3$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{3}$ |
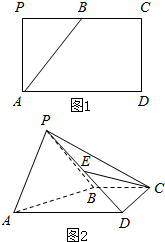 如图1,矩形APCD中,AD=2AP,B为PC的中点,将△APB折沿AB折起,使得PD=PC,如图2.
如图1,矩形APCD中,AD=2AP,B为PC的中点,将△APB折沿AB折起,使得PD=PC,如图2.