题目内容
17.在△ABC中,AB=2,AC=3,BC边上的中线AD=2,则△ABC的面积为$\frac{3\sqrt{15}}{4}$.分析 延长AD至E,使DE=AD,由三角形全等可得△ABC的面积等于△ABE的面积S,解三角形ABE可得cos∠ABE,进而可得sin∠ABE,代入三角形的面积公式可得.
解答 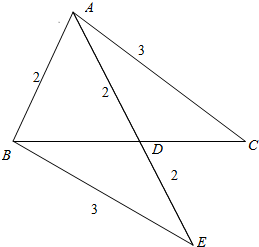 解:由题意延长AD至E,使DE=AD=2,
解:由题意延长AD至E,使DE=AD=2,
可证△BDE≌△CDA,其面积相等,
故△ABC的面积等于△ABE的面积S,
由已知数据可得AB=2,AE=4,BE=AC=3,
在△ABE中由余弦定理可得cos∠ABE=$\frac{{2}^{2}+{3}^{2}-{4}^{2}}{2×2×3}$=-$\frac{1}{4}$,
∴sin∠ABE=$\sqrt{1-co{s}^{2}∠ABE}$=$\frac{\sqrt{15}}{4}$,
∴S=$\frac{1}{2}$×2×3×$\frac{\sqrt{15}}{4}$=$\frac{3\sqrt{15}}{4}$
故答案为:$\frac{3\sqrt{15}}{4}$
点评 本题考查余弦定理解三角形,作辅助线把三角形的面积进行转化是解决问题的关键,属中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
7. 读程序
读程序
对甲乙两程序和输出结果判断正确的是( )
 读程序
读程序对甲乙两程序和输出结果判断正确的是( )
| A. | 程序不同,结果不同 | B. | 程序相同,结果不同 | ||
| C. | 程序不同,结果相同 | D. | 程序相同,结果相同 |
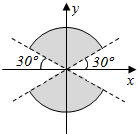 已知角β的终边在图中阴影所表示的范围内(不包括边界),那么β∈(K•180°+30°,K•180°+150°),k∈Z..
已知角β的终边在图中阴影所表示的范围内(不包括边界),那么β∈(K•180°+30°,K•180°+150°),k∈Z..