题目内容
15.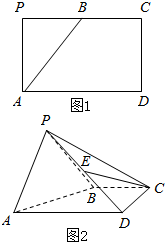 如图1,矩形APCD中,AD=2AP,B为PC的中点,将△APB折沿AB折起,使得PD=PC,如图2.
如图1,矩形APCD中,AD=2AP,B为PC的中点,将△APB折沿AB折起,使得PD=PC,如图2.(1)若E为PD中点,证明:CE∥平面APB;
(2)证明:平面APB⊥平面ABCD.
分析 (1)取PA中点F,连接EF,BF,由已知条件推导出EFBC为平行四边形,由此能证明CE∥平面APB.
(2)取CD中点G,AB中点H,连接PG,HG,PH,由已知条件推导出PG⊥CD,PH⊥AB,BC⊥CD,从而HG⊥CD,由线面垂直得CD⊥PH.由此能证明PH⊥平面ABCD.
解答  证明:(1)取PA中点F,连接EF,BF,
证明:(1)取PA中点F,连接EF,BF,
因为E为PD中点,所以EF平行且等于$\frac{1}{2}$AD,
因为BCEF平行且等于$\frac{1}{2}$AD,
所以EFEF平行且等于BC,所以EFBC为平行四边形,
所以BF∥CE,…(4分)
因为BF?平面APB,CE不包含于平面APB,
所以CE∥平面APB.…(6分)
(2)取CD中点G,AB中点H,连接PG,HG,PH,
∵PC=PD,CD中点G,∴PG⊥CD,
∵△APB是等腰三角形,H是AB中点,
∴PH⊥AB,HG∥AD.∵BC∥AD,BC⊥CD,∴HG⊥CD,…(10分)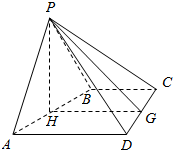
HG∩PG=G,HG?平面PHG,PG?平面PHG,
∴CD⊥平面PHG.PH?平面PHG,∴CD⊥PH.
∵AB?平面ABCD,CD?平面ABCD,AB和CD相交,
∴PH⊥平面ABCD.
又PH?平面APB,
∴平面APB⊥平面ABCD. …(12分)
点评 本题考查直线与平面平行的证明,考查直线与平面垂直的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
20.已知集合P={a|a=$\frac{kπ}{2}$,k∈Z},则下列集合与集合P相等的是( )
| A. | {a|a=kπ+$\frac{π}{2}$,k∈Z} | B. | {a|a=kπ,k∈Z} | ||
| C. | {a|a=2kπ+$\frac{π}{2}$,k∈Z} | D. | {a|a=kπ或a=kπ+$\frac{π}{2}$,k∈Z} |
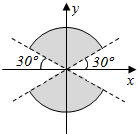 已知角β的终边在图中阴影所表示的范围内(不包括边界),那么β∈(K•180°+30°,K•180°+150°),k∈Z..
已知角β的终边在图中阴影所表示的范围内(不包括边界),那么β∈(K•180°+30°,K•180°+150°),k∈Z..