题目内容
18.根据条件利用单位圆写出θ的取值范围:(1)cosθ<$\frac{\sqrt{2}}{2}$;
(2)$\frac{1}{2}$≤sinθ<$\frac{\sqrt{3}}{2}$.
分析 根据题意,画出单位圆,得出单位圆中cosθ=$\overrightarrow{OM}$,sinθ=$\overrightarrow{MA}$,再根据不等式求出θ的取值范围.
解答 解:(1)根据题意,画出图形,如图所示,
在单位圆中cosθ=$\overrightarrow{OM}$,
且cosθ<$\frac{\sqrt{2}}{2}$在[0,2π]的角是$\frac{π}{4}$<θ<$\frac{7π}{4}$,
∴θ的取值范围是:$\frac{π}{4}$+2kπ<θ<$\frac{7π}{4}$+2kπ,k∈Z;
(2)根据题意,画出图形,如图2所示,
在单位圆中,sinθ=$\overrightarrow{MA}$,
∴$\frac{1}{2}$≤sinθ<$\frac{\sqrt{3}}{2}$在[0,2π]的角是$\frac{π}{6}$≤θ<$\frac{π}{3}$,或$\frac{2π}{3}$<θ≤$\frac{5π}{6}$,
∴θ的取值范围是:$\frac{π}{6}$+2kπ≤θ<$\frac{π}{3}$+2kπ,或$\frac{2π}{3}$+2kπ<θ≤$\frac{5π}{6}$+2kπ,k∈Z.
点评 本题考查了利用单位圆中的三角函数线求满足条件的角的集合的应用问题,是基础题目.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
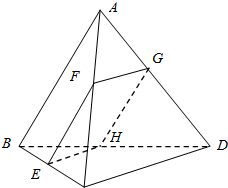 如图所示,在四面体ABCD中,截面EFGH平行于对于棱AB和CD,试问截面在什么位置时其截面面积最大?
如图所示,在四面体ABCD中,截面EFGH平行于对于棱AB和CD,试问截面在什么位置时其截面面积最大?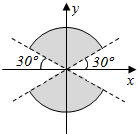 已知角β的终边在图中阴影所表示的范围内(不包括边界),那么β∈(K•180°+30°,K•180°+150°),k∈Z..
已知角β的终边在图中阴影所表示的范围内(不包括边界),那么β∈(K•180°+30°,K•180°+150°),k∈Z..