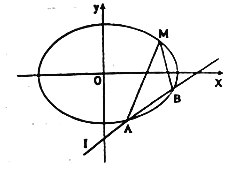
[题目]已知椭圆的中心在原点.焦点在轴上.离心率为.且经过点.直线: 交椭圆于. 两不同的点.(1)求椭圆的方程,(2)若直线不过点.求证:直线. 与轴围成等腰三角形. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知椭圆的中心在原点，焦点在轴上，离心率为，且经过点，直线：交椭圆于，两不同的点.

（1）求椭圆的方程；

（2）若直线不过点，求证：直线，与轴围成等腰三角形.

【答案】（1）；（2）；（3）证明详见解析．

【解析】试题分析：（Ⅰ）求椭圆方程采用待定系数法，首先设出椭圆方程，由离心率和点的坐标可分别得到关于的关系式，结合可求得值，从而得到椭圆方程；（Ⅱ）将直线方程与椭圆方程联立，借助于二次方程根与系数的关系可得到坐标与的关系式，证明三角形为等腰三角形转化为证明直线的斜率互为相反数，通过计算两斜率之和为0，来实现结论的证明.

（Ⅰ）设椭圆方程为，因为，所以，

又椭圆过点，所以，解得，，故椭圆的方程为

（Ⅱ）将代入并整理得，

再根据，求得.

设直线，斜率分别为和，只要证即可.

设，，则，，

∴

而此分式的分子等于

可得

因此，与轴所围成的三角形为等腰三角形.

练习册系列答案

相关题目

【题目】在某单位的职工食堂中，食堂每天以元/个的价格从面包店购进面包，然后以元/个的价格出售．如果当天卖不完，剩下的面包以元/个的价格卖给饲料加工厂．根据以往统计资料，得到食堂每天面包需求量的频率分布直方图如下图所示．食堂某天购进了90个面包，以（单位：个，）表示面包的需求量，（单位：元）表示利润．

（Ⅰ）求关于的函数解析式；

（Ⅱ）根据直方图估计利润不少于元的概率；

（III）在直方图的需求量分组中，以各组的区间中点值代表该组的各个值，并以需求量落入该区间的频率作为需求量取该区间中间值的概率(例如：若需求量，则取，且的概率等于需求量落入的频率)，求的分布列和数学期望．

【题目】在四棱锥中，平面，，，，，为的中点，为棱上一点．

（Ⅰ）当为何值时，有平面；

（Ⅱ）在（Ⅰ）的条件下，求点到平面的距离．

【题目】已知二次函数f（x）=x2+bx+c，当x∈R时f（x）=f（2﹣x）恒成立，且3是f（x）的一个零点．（Ⅰ）求函数f（x）的解析式；
（Ⅱ）设g（x）=f（ax）（a＞1），若函数g（x）在区间[﹣1，1]上的最大值等于5，求实数a的值．

【题目】已知定义在区间（0，+∞）上的函数f（x）=|t（x+ ）﹣5|，其中常数t＞0．
（1）若函数f（x）分别在区间（0，2），（2，+∞）上单调，试求实数t的取值范围；
（2）当t=1时，方程f（x）=m有四个不相等的实根x1 ， x2 ， x3 ， x4 ． ①求四根之积x1x2x3x4的值；
②在[1，4]上是否存在实数a，b（a＜b），使得f（x）在[a，b]上单调且取值范围为[ma，mb]？若存在，求出m的取值范围；若不存在，请说明理由．