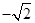题目内容
已知函数f(x)=x3+ax2+bx.
(1)若函数y=f(x)在x=2处有极值-6,求y=f(x)的单调递减区间;
(2)若y=f(x)的导数f′(x)对x∈[-1,1]都有f′(x)≤2,求 的取值范围.
的取值范围.
(1)若函数y=f(x)在x=2处有极值-6,求y=f(x)的单调递减区间;
(2)若y=f(x)的导数f′(x)对x∈[-1,1]都有f′(x)≤2,求
 的取值范围.
的取值范围.(1)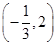 (2)(-∞,-2)∪[1,+∞)
(2)(-∞,-2)∪[1,+∞)
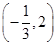 (2)(-∞,-2)∪[1,+∞)
(2)(-∞,-2)∪[1,+∞)(1)f′(x)=3x2+2ax+b,
依题意有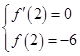 ,即
,即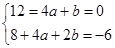
解得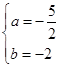 ,∴f′(x)=3x2-5x-2.
,∴f′(x)=3x2-5x-2.
由f′(x)<0,得-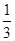 <x<2.
<x<2.
∴y=f(x)的单调递减区间是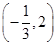 .
.
(2)由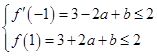 ,得
,得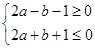
不等式组确定的平面区域如图阴影部分所示:
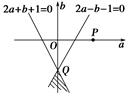
由 ,得
,得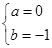
∴Q点的坐标为(0,-1).
设z= ,则z表示平面区域内的点(a,b)与点
,则z表示平面区域内的点(a,b)与点
P(1,0)连线的斜率.
∵kPQ=1,由图可知z≥1或z<-2,
即 ∈(-∞,-2)∪[1,+∞).
∈(-∞,-2)∪[1,+∞).
依题意有
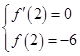 ,即
,即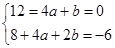
解得
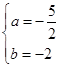 ,∴f′(x)=3x2-5x-2.
,∴f′(x)=3x2-5x-2.由f′(x)<0,得-
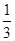 <x<2.
<x<2.∴y=f(x)的单调递减区间是
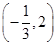 .
.(2)由
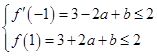 ,得
,得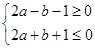
不等式组确定的平面区域如图阴影部分所示:

由
 ,得
,得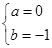
∴Q点的坐标为(0,-1).
设z=
 ,则z表示平面区域内的点(a,b)与点
,则z表示平面区域内的点(a,b)与点P(1,0)连线的斜率.
∵kPQ=1,由图可知z≥1或z<-2,
即
 ∈(-∞,-2)∪[1,+∞).
∈(-∞,-2)∪[1,+∞).
练习册系列答案
相关题目
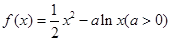 .
.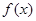 在
在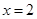 处的切线与直线
处的切线与直线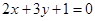 垂直,求
垂直,求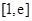 上的最大值.
上的最大值.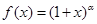 的定义域是
的定义域是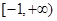 ,其中常数
,其中常数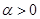 .
.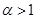 ,求
,求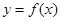 的过原点的切线方程.
的过原点的切线方程.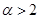 时,求最大实数
时,求最大实数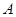 ,使不等式
,使不等式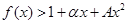 对
对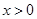 恒成立.
恒成立.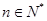 ,有
,有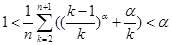 .
.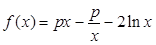 .
.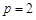 ,求曲线
,求曲线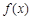 在点
在点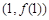 处的切线方程;
处的切线方程;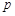 的取值范围;
的取值范围;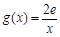 ,若在
,若在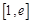 上至少存在一点
上至少存在一点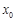 ,使得
,使得 成立,求实数
成立,求实数 ,
, (
( 为常数).
为常数). 的图象在点
的图象在点 处的切线与函数
处的切线与函数 的图象相切,求实数
的图象相切,求实数 ,
, ,
, 、
、 使得
使得 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数 ;
; 时,若对于区间
时,若对于区间 内的任意两个不相等的实数
内的任意两个不相等的实数 、
、 ,都有
,都有
 成立,求
成立,求 的图像在点
的图像在点 处的切线方程是
处的切线方程是 ,则
,则 _____.
_____.
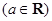 .
.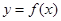 在点
在点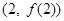 处的切线方程是y=x+ln2时,求a的值.
处的切线方程是y=x+ln2时,求a的值. ,则
,则 在
在 处的导数
处的导数 ( )
( )