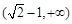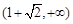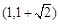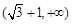题目内容
已知椭圆
+
=1的左、右焦点分别为F1、F2,点P在椭圆上.若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为( )
| x2 |
| 16 |
| y2 |
| 9 |
A.
| B.3 | C.
| D.
|
设椭圆短轴的一个端点为M.
由于a=4,b=3,
∴c=
<b
∴∠F1MF2<90°,
∴只能∠PF1F2=90°或∠PF2F1=90°.
令x=±
得
y2=9(1-
)=
,
∴|y|=
.
即P到x轴的距离为
.
由于a=4,b=3,
∴c=
| 7 |
∴∠F1MF2<90°,
∴只能∠PF1F2=90°或∠PF2F1=90°.
令x=±
| 7 |
y2=9(1-
| 7 |
| 16 |
| 92 |
| 16 |
∴|y|=
| 9 |
| 4 |
即P到x轴的距离为
| 9 |
| 4 |

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
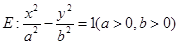 的两条渐近线分别为
的两条渐近线分别为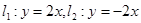 .
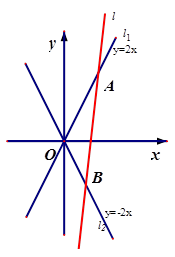
.
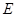 的离心率;
的离心率;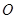 为坐标原点,动直线
为坐标原点,动直线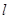 分别交直线
分别交直线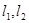 于
于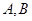 两点(
两点(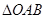 的面积恒为8,试探究:是否存在总与直线
的面积恒为8,试探究:是否存在总与直线 ,则C的实轴长为( )
,则C的实轴长为( )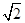
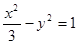 的焦距为( ).
的焦距为( ). 
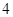
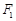 ,
,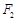 分别是双曲线
分别是双曲线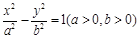 的左、右焦点,过点
的左、右焦点,过点 轴的直线与双曲线交于
轴的直线与双曲线交于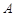 ,
,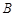 两点,若
两点,若 是钝角三角形,则该双曲线离心率的取值范围是
是钝角三角形,则该双曲线离心率的取值范围是