题目内容
1．已知A={x∈R|x2-2x-8=0}，B={x∈R|x2+ax+a2-12=0}，B是A的非空子集，求实数a的值．分析 解一元二次方程求得集合A，由B是A的非空子集，分类讨论，分别求出实数a的取值．
解答 解：由已知，A={-2，4}．
∵B是A的非空子集，∴B={-2}或{4}或{-2，4}．
若B={-2}，则有$\left\{\begin{array}{l}{-2-2=-a}\\{（-2）（-2）={a}^{2}-12}\end{array}\right.$，解得：a=4；
若B={4}，则有$\left\{\begin{array}{l}{4+4=-a}\\{4×4={a}^{2}-12}\end{array}\right.$，解得a∈∅；
若B={-2，4}，由韦达定理可得$\left\{\begin{array}{l}{-2+4=-a}\\{（-2）×4={a}^{2}-12}\end{array}\right.$，解得a=-2
综上，所求实数a的值为-2或4．
点评 本题主要考查集合关系中参数的取值范围问题，一元二次方程的解法，体现了分类讨论的数学思想，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
11．设an=$\frac{|sin1|}{2}$+$\frac{|sin2|}{{2}^{2}}$+…+$\frac{|sinn|}{{2}^{n}}$，则对任意正整数m，n（m＞n）都成立的是（ ）
| A． | am-an＜$\frac{1}{{2}^{n}}$ | B． | am-an＞$\frac{1}{{2}^{n}}$ | C． | am-an＜$\frac{1}{{2}^{m}}$ | D． | am-an＞$\frac{m-n}{2}$ |
16．在半径为1的圆周上随机选取三点，它们构成一个锐角三角形的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
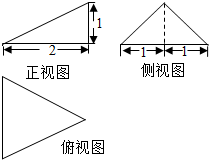某三棱锥的三视图如图所示，则该三棱锥的4个面中，直角三角形的个数是1个，它的表面积是21．
如图，已知圆C的圆心在y轴的正半轴上，且与x轴相切，圆C与直线y=kx+3相交于A，B两点．当$k=\sqrt{3}$时，$|AB|=\sqrt{15}$．