题目内容
设f(x)是以2为周期的奇函数,且f(- )=3,若sinα=
)=3,若sinα= ,则f(4cos2α)= ( )
,则f(4cos2α)= ( )
| A.-3 | B.3 | C.- | D.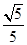 |
A
解析试题分析:因为,f(x)是以2为周期的奇函数,且f(-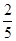 )="3," sinα=
)="3," sinα=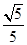 ,
,
所以,f(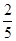 )=-3,
)=-3,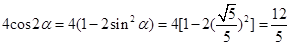 ,
,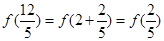 =-3,故选A。
=-3,故选A。
考点:本题主要考查函数的奇偶性、周期性,三角函数的同角公式、倍半公式。
点评:中档题,本题综合性较强,主要考查函数的奇偶性、周期性,三角函数的同角公式、倍半公式,注意运用转化思想求解。

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
函数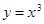 ( )
( )
A.是奇函数,且在 上是单调增函数 上是单调增函数 |
B.是奇函数,且在 上是单调减函数 上是单调减函数 |
C.是偶函数,且在 上是单调增函数 上是单调增函数 |
D.是偶函数,且在 上是单调减函数 上是单调减函数 |
在下列区间中,函数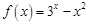 的零点所在区间是( )
的零点所在区间是( )
A.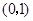 | B.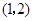 | C.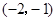 | D.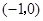 |
已知函数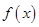 是R上的奇函数,若对于
是R上的奇函数,若对于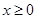 ,都有
,都有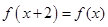 ,
, 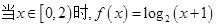 时,
时,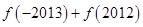 的值为
的值为
A.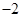 | B.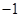 | C.1 | D.2 |
设函数 是定义在
是定义在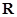 上的以
上的以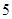 为周期的偶函数,若
为周期的偶函数,若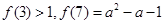 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A.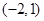 | B.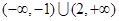 | C.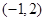 | D.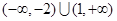 |
已知函数 满足
满足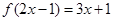 ,则
,则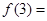 ( )
( )
A.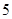 | B.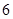 | C.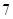 | D.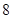 |
已知偶函数 在区间
在区间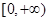 上是增函数,如果
上是增函数,如果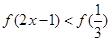 ,则
,则 的取值范围是( )
的取值范围是( )
A.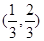 | B.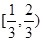 | C.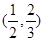 | D. |
使得函数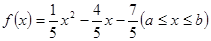 的值域为
的值域为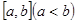 的实数对
的实数对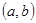
有( )对
| A.1 | B.2 | C.3 | D.无数 |
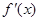 是函数
是函数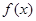 的导函数,将
的导函数,将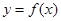 和
和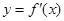 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )