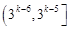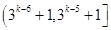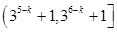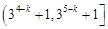题目内容
使得函数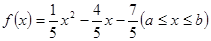 的值域为
的值域为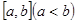 的实数对
的实数对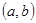
有( )对
| A.1 | B.2 | C.3 | D.无数 |
B
解析试题分析: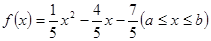 为开口向上的抛物线,所以x在[2,+∞)上单调递增,在(-∞,2]上单调递减
为开口向上的抛物线,所以x在[2,+∞)上单调递增,在(-∞,2]上单调递减
(1) 2≤a<b,此时[a,b]在f(x)的单调增区间上则最大值b=f(b),最小值a=f(a),即a、b为方程x=f(x)的两根。
x=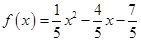 ,即
,即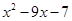 =0的两根为a、b,
=0的两根为a、b,
由韦达定理,ab=-7,即a、b异号,这与0<2<a<b矛盾,所以这种情况不可能。
(2) a<b≤2,此时[a,b]在f(x)的单调减区间上,
则最大值b=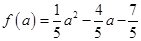 ①,最小值a=
①,最小值a=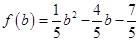 ②
②
由①-②,得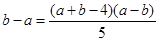 ,
,
由于a<b,所以a-b≠0,可得-1=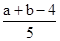 ,a+b=-1可得a=-1-b,将其代入①,得
,a+b=-1可得a=-1-b,将其代入①,得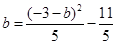 且b=-1-a,将其代入②,的
且b=-1-a,将其代入②,的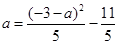 , 则a、b为方程
, 则a、b为方程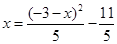 的两根,
的两根,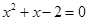 ,解得x=1,-2,由于a<b,所以a=-2,b=1,满足a<b≤2,所以(a,b)=(-2,1)是一组解。
,解得x=1,-2,由于a<b,所以a=-2,b=1,满足a<b≤2,所以(a,b)=(-2,1)是一组解。
(3) a<2<b,此时[a,b]包含x=2
则最小值a=f(2)=-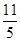 ,满足a<2,而f(x)在[a,2]上单调减,在[2,b]上单调增
,满足a<2,而f(x)在[a,2]上单调减,在[2,b]上单调增
所以最大值为f(a)或f(b),最大值须进一步分类讨论:
注意到|a-2|=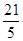 ,所以进行如下分类:
,所以进行如下分类:
1° |b-2|>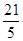 ,即b>
,即b>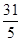
此时由于|b-2|>|a-2|,f(b)= 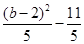 >f(a)=
>f(a)= 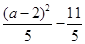 即最大值,
即最大值,
b="f(b)=" 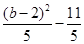 ,
,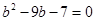 ,解得b=
,解得b=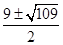 其中b=
其中b=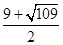 满足b>
满足b>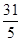 ,
,
所以(a,b)="(" 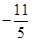 ,
, 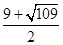 )是另一组解;
)是另一组解;
2° |b-2|<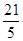 ,即2<b<
,即2<b<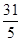 。此时由于|b-2|<|a-2|,
。此时由于|b-2|<|a-2|,
f(b)= 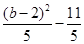 <f(a)=
<f(a)= 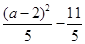 ,
,
即最大值b=f(a)=f(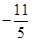 )=
)=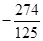 <0,与b>2矛盾,所以这种情况不可能;
<0,与b>2矛盾,所以这种情况不可能;
综上所述,满足题意的(a,b)有2对,故选 B.
考点:本题主要考查二次函数的图象和性质,分类讨论思想。
点评:难题,涉及二次函数值域问题,关注图象的开口方向、对称轴位置、区间端点函数值,均为基本方法。本题分类讨论易于出错,特别是第三种情况下。

设f(x)是以2为周期的奇函数,且f(-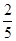 )=3,若sinα=
)=3,若sinα=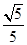 ,则f(4cos2α)= ( )
,则f(4cos2α)= ( )
| A.-3 | B.3 | C.-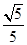 | D.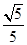 |
函数f(x)=ln(4+3x-x2)的单调递减区间是
A.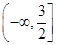 | B.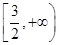 | C.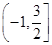 | D.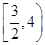 |
函数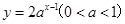 的图象一定过点( )
的图象一定过点( )
| A.(1,1) | B.(1,2) | C.(2,0) | D.(2,-1) |
函数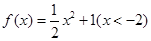 的反函数是
的反函数是
A.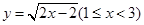 | B.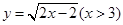 |
C.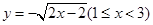 | D.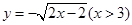 |
已知函数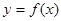 的导函数
的导函数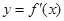 的图像如下,则( )
的图像如下,则( )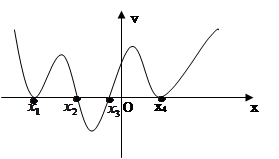
A.函数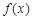 有1个极大值点,1个极小值点 有1个极大值点,1个极小值点 |
B.函数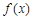 有2个极大值点,2个极小值点 有2个极大值点,2个极小值点 |
C.函数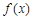 有3个极大值点,1个极小值点 有3个极大值点,1个极小值点 |
D.函数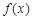 有1个极大值点,3个极小值点 有1个极大值点,3个极小值点 |
设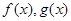 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当 时,
时,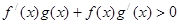 ,且
,且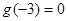 ,则
,则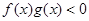 的解集是( )
的解集是( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D. (-∞,-3)∪(0,3) |
如果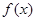 为偶函数,且
为偶函数,且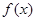 导数存在,则
导数存在,则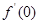 的值为 ( )
的值为 ( )
| A.2 | B.1 | C.0 | D.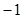 |
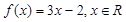 规定:给出一个实数
规定:给出一个实数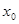 ,赋值
,赋值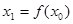 ,若
,若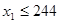 ,则继续赋值
,则继续赋值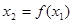 , ,
, , 以此类推,若
以此类推,若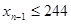 ,则
,则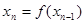 ,否则停止赋值,如果得到
,否则停止赋值,如果得到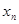 称为赋值了
称为赋值了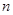 次
次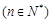 .已知赋值了
.已知赋值了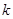 次后停止,则
次后停止,则