题目内容
【题目】如图,在平面四边形ABCD中, ![]() .
.
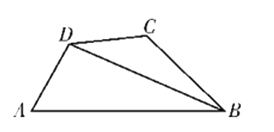
(1)若![]() ,求
,求![]() 的大小;
的大小;
(2)设△BCD的面积为S,求S的取值范围.
【答案】(1) ![]() . (2)
. (2) ![]()
【解析】
(1)在△ABD中,由余弦定理可求BD的值,进而在△BCD中,由正弦定理可求sin∠CDB![]() ,求得∠CDB,即可得解∠CBD=60°﹣∠CDB=15°.
,求得∠CDB,即可得解∠CBD=60°﹣∠CDB=15°.
(2)设∠CBD=θ,则∠CDB=60°﹣θ.在△BCD中,由正弦定理可求BC=4sin(60°﹣θ),利用三角形面积公式,三角函数恒等变换的应用可求S=2![]() sin(2θ+30°)
sin(2θ+30°)![]() ,结合范围0°<θ<60°,利用正弦函数的性质可求S的取值范围.
,结合范围0°<θ<60°,利用正弦函数的性质可求S的取值范围.
(1)
在![]() 中,因为
中,因为![]() ,
,
则![]() ,所以
,所以![]() .
.
在![]() 中,因为
中,因为![]() ,
,
由![]() ,得
,得![]() ,则
,则![]() .
.
所以![]() .
.
(2)设![]() ,则
,则![]() .
.
在![]() 中,因为
中,因为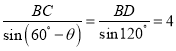 ,则
,则![]() .
.
所以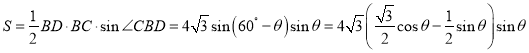
![]()
![]() .
.
因为![]() ,则
,则![]() ,所以
,所以![]() .
.
故![]() 的取值范围是
的取值范围是![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目