题目内容
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ ![]() 与以原点为圆心,以椭圆C的短半轴为半径的圆相切,F1 , F2为其左右焦点,P为椭圆C上的任意一点,△F1PF2的重心为G,内心为I,且IG∥F1F2 .
与以原点为圆心,以椭圆C的短半轴为半径的圆相切,F1 , F2为其左右焦点,P为椭圆C上的任意一点,△F1PF2的重心为G,内心为I,且IG∥F1F2 .
(1)求椭圆C的方程;
(2)已知A为椭圆C上的左顶点,直线∫过右焦点F2与椭圆C交于M,N两点,若AM,AN的斜率k1 , k2满足k1+
k2=﹣ ![]() ,求直线MN的方程.
,求直线MN的方程.
【答案】
(1)解:设P(x0,y0),I(x1,y1),则G( ![]() ).
).
又IG∥F1F2, ![]() ,|F1F2|=2c,
,|F1F2|=2c,
∴ ![]() =
= ![]() |F1F2||y0|=
|F1F2||y0|= ![]() .
.
∴2c= ![]() ,故a=2c.
,故a=2c.
又直线y=x+ ![]() 与以原点为圆心,以椭圆C的短半轴为半径的圆相切,
与以原点为圆心,以椭圆C的短半轴为半径的圆相切,
∴b= ![]() =
= ![]() ,
,
∴a=2,c=1.∴ ![]() .
.
(2)解:若直线l斜率不存在,显然k1+k2=0不合题意;
则直线l的斜率存在.
设直线l为y=k(x﹣1),直线l和椭圆交于M(x1,y1),N(x2,y2).
将y=k(x﹣1)代入3x2+4y2=12中,得:
(3+4k2)x2﹣8k2x+4k2﹣12=0,
依题意:△=9k2+9>0,
由韦达定理知: 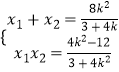 ,
,
又kAM+kAN= ![]() =k(
=k( ![]() )
)
=k[2﹣3( ![]() )],
)],
![]() =
= ![]()
= ![]()
= ![]() ,
,
从而kAM+kAN=k(2﹣3 ![]() )=﹣
)=﹣ ![]() ,
,
解得k=2,符合△>0.
故所求直线MN的方程为:y=2(x﹣1)
【解析】(1)设P(x0 , y0),I(x1 , y1),则G( ![]() ),由已知条件推导出a=2c,b=
),由已知条件推导出a=2c,b= ![]() =
= ![]() 由此能求出椭圆方程.(2)设直线l为y=k(x﹣1),直线l和椭圆交于M(x1 , y1),N(x2 , y2).将y=k(x﹣1)代入3x2+4y2=12中,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用韦达定理能求出直线MN的方程.
由此能求出椭圆方程.(2)设直线l为y=k(x﹣1),直线l和椭圆交于M(x1 , y1),N(x2 , y2).将y=k(x﹣1)代入3x2+4y2=12中,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用韦达定理能求出直线MN的方程.

 阅读快车系列答案
阅读快车系列答案