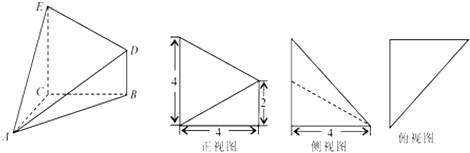
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΕ·‘≤QΙΐΕ®ΒψFΘ®0Θ§©¹1Θ©Θ§«“”κ÷±œΏy=1œύ«–ΘΜΆ÷‘≤NΒΡΕ‘≥Τ÷αΈΣΉχ±ξ÷αΘ§÷––ΡΈΣΉχ±ξ‘≠ΒψOΘ§F «Τδ“ΜΗωΫΙΒψΘ§”÷ΒψΘ®0Θ§2Θ©‘ΎΆ÷‘≤N…œΘ°
Θ®1Θ©«σΕ·‘≤‘≤–ΡQΒΡΙλΦΘMΒΡΖΫ≥ΧΚΆΆ÷‘≤NΒΡΖΫ≥ΧΘΜ
Θ®2Θ©ΙΐΒψΘ®0Θ§©¹4Θ©Ής÷±œΏlΫΜΙλΦΘM”ΎAΘ§BΝΫΒψΘ§Ν§ΫαOAΘ§OBΘ§…δœΏOAΘ§OBΫΜΆ÷‘≤N”ΎCΘ§DΝΫΒψΘ§«σΓςOCDΟφΜΐΒΡΉν–Γ÷ΒΘ°
Θ®3Θ©ΗΫΦ”ΧβΘΚΙΐΆ÷‘≤N…œ“ΜΕ·ΒψPΉς‘≤x2+Θ®y©¹1Θ©2=1ΒΡΝΫΧθ«–œΏΘ§«–ΒψΖ÷±πΈΣGΘ§HΘ§«σ ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚ“άΧβ“βΘ§”…≈ΉΈοœΏΒΡΕ®“ε“ΉΒΟΕ·ΒψQΒΡΙλΦΘMΒΡ±ξΉΦΖΫ≥ΧΈΣΘΚx2=©¹4yΘ§
“άΧβ“βΩ……ηΆ÷‘≤NΒΡ±ξΉΦΖΫ≥ΧΈΣ ![]() +
+ ![]() =1Θ®aΘΨbΘΨ0Θ©Θ§
=1Θ®aΘΨbΘΨ0Θ©Θ§
œ‘»Μ”–c=1Θ§a=2Γύb= ![]() Θ§
Θ§
ΓύΆ÷‘≤NΒΡ±ξΉΦΖΫ≥ΧΈΣΘΚ ![]() ΘΜ
ΘΜ
ΙλΦΘ ![]()
Θ®2Θ©ΫβΘΚ 
Υυ“‘x1x2+y1y2=0OAΓΆOB
…η ![]() Θ§
Θ§
Υυ“‘ ![]() Θ§
Θ§
Ά§άμΩ…ΒΟΘΚ ![]() Θ§
Θ§
Υυ“‘ ![]() Θ§
Θ§
Ννt=1+k2Θ®tΓί1Θ©Θ§ 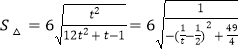 Θ§
Θ§
Υυ“‘Β± ![]()
Θ®3Θ©ΫβΘΚ…ηΓœGPH=2ΠΝΘ§‘≤x2+Θ®y©¹1Θ©2=1ΒΡ‘≤–ΡΈΣEΘ§»γΆΦΘΚ
Β±P‘ΎΆ÷‘≤…œΕΞΒψ ±PEΉν–ΓΈΣ1Θ§‘ΎΆ÷‘≤œ¬ΕΞΒψ ±Θ§|PE|ΒΡΉν¥σ÷ΒΈΣ3Θ§PEΓ [1Θ§3]Θ§
PEcosΠΝ=PGΘ§sinΠΝ= ![]() Θ°
Θ°
Γύ 
= 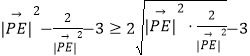 =
= ![]() Θ§Β±«“ΫωΒ±|PE|=
Θ§Β±«“ΫωΒ±|PE|= ![]() ±»ΓΒ»Κ≈Θ°
±»ΓΒ»Κ≈Θ°
“ρΈΣ|PE|Γ [1Θ§3]Θ§Υυ“‘ ![]() Θ°
Θ°
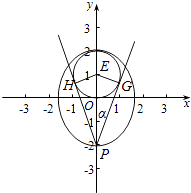
ΓΨΫβΈωΓΩΘ®1Θ©”…≈ΉΈοœΏΒΡΕ®“εΩ…ΒΟΕ·ΒψQΒΡΙλΦΘMΒΡ±ξΉΦΖΫ≥ΧΘ§”…Χβ“βΩ…ΒΟc=1Θ§a=2Θ§«σΒΟbΘ§ΫχΕχΒΟΒΫΆ÷‘≤ΖΫ≥ΧΘΜΘ®2Θ©œ‘»Μ÷±œΏmΒΡ–±¬ ¥φ‘ΎΘ§≤ΜΖΝ…η÷±œΏmΒΡ÷±œΏΖΫ≥ΧΈΣΘΚy=kx©¹4Θ§Ζ÷±π¥ζ»κ≈ΉΈοœΏΖΫ≥ΧΚΆΆ÷‘≤ΖΫ≥ΧΘ§‘Υ”ΟΈΛ¥οΕ®άμΚΆœ“≥ΛΙΪ ΫΘ§“‘ΦΑΒψΒΫ÷±œΏΒΡΨύάκΙΪ ΫΘ§«σΒΟ»ΐΫ«–ΈΒΡΟφΜΐΘ§‘Ό”…≤ΜΒ» ΫΒΡ–‘÷ Θ§Φ¥Ω…ΒΟΒΫΥυ«σΉν–Γ÷ΒΘ°Θ®3Θ©…ηΓœEPF=2ΠΝΘ§«σ≥ω ![]() ±μ¥ο ΫΘ§άϊ”Ο
±μ¥ο ΫΘ§άϊ”Ο ![]() ΒΡΖΕΈßΘ§«σΫβ±μ¥ο ΫΒΡΖΕΈßΦ¥Ω…Θ°
ΒΡΖΕΈßΘ§«σΫβ±μ¥ο ΫΒΡΖΕΈßΦ¥Ω…Θ°
ΓΨΩΦΒψΨΪΈωΓΩ±ΨΧβ÷ς“ΣΩΦ≤ιΝΥΆ÷‘≤ΒΡ±ξΉΦΖΫ≥ΧΒΡœύΙΊ÷Σ ΕΒψΘ§–η“Σ’ΤΈ’Ά÷‘≤±ξΉΦΖΫ≥ΧΫΙΒψ‘Ύx÷αΘΚ![]() Θ§ΫΙΒψ‘Ύy÷αΘΚ
Θ§ΫΙΒψ‘Ύy÷αΘΚ![]() ≤≈Ρή’ΐ»ΖΫβ¥π¥ΥΧβΘ°
≤≈Ρή’ΐ»ΖΫβ¥π¥ΥΧβΘ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥ΧΊ…Ϊ≤ΆΙίΩΣΆ®ΝΥΟάΆ≈Άβ¬τΖΰΈώΘ§‘Ύ“Μ÷ήΡΎΒΡΡ≥ΧΊ…Ϊ≤ΥΆβ¬τΖί ΐ![]() Θ®ΖίΘ©”κ ’»κ
Θ®ΖίΘ©”κ ’»κ![]() Θ®‘ΣΘ©÷°Φδ”–»γœ¬ΒΡΕ‘”Π ΐΨίΘΚ
Θ®‘ΣΘ©÷°Φδ”–»γœ¬ΒΡΕ‘”Π ΐΨίΘΚ
Άβ¬τΖί ΐ | 2 | 4 | 5 | 6 | 8 |
’»κ | 30 | 40 | 60 | 50 | 70 |

Θ®1Θ©Μ≠≥ω…ΔΒψΆΦΘΜ
Θ®2Θ©«σΜΊΙι÷±œΏΖΫ≥ΧΘΜ
Θ®3Θ©Ψί¥ΥΙάΦΤΆβ¬τΖί ΐΈΣ12Ζί ±Θ§ ’»κΈΣΕύ…Ό‘ΣΘ°
ΉΔΘΚΔΌ≤ΈΩΦΙΪ ΫΘΚœΏ–‘ΜΊΙιΖΫ≥ΧœΒ ΐΙΪ Ϋ Θ§
Θ§ ![]() ΘΜ
ΘΜ
ΔΎ≤ΈΩΦ ΐΨίΘΚ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ°
Θ°