题目内容
(本小题满分12 分)
分)
设函数f(x)的定义域为R,若|f(x)|≤|x|对任意的实数x均成立,则称函数f(x)为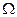 函数。
函数。
(1)试判断函数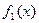 =
=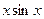
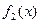 =
=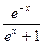 中哪些是
中哪些是 函数,并说明理由;
函数,并说明理由;
(2)求证:若a>1,则函数f(x)=ln(x2+a)-lna是 函数。
函数。
 分)
分)设函数f(x)的定义域为R,若|f(x)|≤|x|对任意的实数x均成立,则称函数f(x)为
 函数。
函数。(1)试判断函数
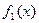 =
=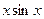
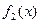 =
=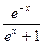 中哪些是
中哪些是 函数,并说明理由;
函数,并说明理由;(2)求证:若a>1,则函数f(x)=ln(x2+a)-lna是
 函数。
函数。(1)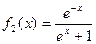 不是
不是 函数;(2)在R上恒有|f(x)| ≤|x|成立,则函数f(x) 是
函数;(2)在R上恒有|f(x)| ≤|x|成立,则函数f(x) 是 函数.
函数.
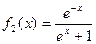 不是
不是 函数;(2)在R上恒有|f(x)| ≤|x|成立,则函数f(x) 是
函数;(2)在R上恒有|f(x)| ≤|x|成立,则函数f(x) 是 函数.
函数.(1)∵|xsinx|≤|x|,∴f1(x)=xsinx是 函数;
函数;
∵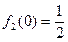 ,∴不满足|f(0)|≤|0|,
,∴不满足|f(0)|≤|0|,
∴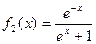 不是
不是 函数;………………………………4分
函数;………………………………4分
(2)设F(x) =f(x)-x,则F′(x)=
=f(x)-x,则F′(x)=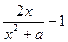
①当x>0时,∵a>1,
∴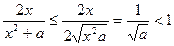
当x=0时,F′(x)=-1<0
∴当x≥0时,F′(x)=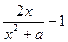 <0.
<0.
∴ F(x)在
F(x)在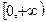 上是减函数………………………………8分
上是减函数………………………………8分
∴F(x)≤F(0),又F(0)=f(0)=0,
∴F(x)=f(x)-x≤0
 ∵x>0时f′(x)=
∵x>0时f′(x)=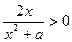
∴函数f(x)在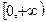 上是增函数,∴f(x)≥f(0)=0
上是增函数,∴f(x)≥f(0)=0
∴0≤f(x)≤x,即|f(x)| ≤|x|
②当x<0时,-x>0, ∴|f(-x)|≤|-x|,显然f(x)为偶函数
∴|f(x)|≤|-x|即|f(x)| ≤|x|
 ∴在R上恒有|f(x)| ≤|x|成立,则函数f(x) 是
∴在R上恒有|f(x)| ≤|x|成立,则函数f(x) 是 函数. ………12分
函数. ………12分
 函数;
函数;∵
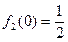 ,∴不满足|f(0)|≤|0|,
,∴不满足|f(0)|≤|0|,∴
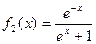 不是
不是 函数;………………………………4分
函数;………………………………4分(2)设F(x)
 =f(x)-x,则F′(x)=
=f(x)-x,则F′(x)=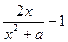
①当x>0时,∵a>1,
∴
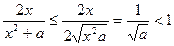
当x=0时,F′(x)=-1<0
∴当x≥0时,F′(x)=
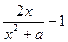 <0.
<0.∴
 F(x)在
F(x)在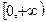 上是减函数………………………………8分
上是减函数………………………………8分∴F(x)≤F(0),又F(0)=f(0)=0,
∴F(x)=f(x)-x≤0
 ∵x>0时f′(x)=
∵x>0时f′(x)=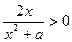
∴函数f(x)在
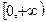 上是增函数,∴f(x)≥f(0)=0
上是增函数,∴f(x)≥f(0)=0∴0≤f(x)≤x,即|f(x)| ≤|x|
②当x<0时,-x>0, ∴|f(-x)|≤|-x|,显然f(x)为偶函数
∴|f(x)|≤|-x|即|f(x)| ≤|x|
 ∴在R上恒有|f(x)| ≤|x|成立,则函数f(x) 是
∴在R上恒有|f(x)| ≤|x|成立,则函数f(x) 是 函数. ………12分
函数. ………12分
练习册系列答案
相关题目
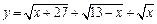 的最大和最小值.
的最大和最小值.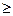 g(x)恒成立,求实数c的取值范围;
g(x)恒成立,求实数c的取值范围;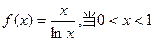 时,下列式子大小关系正确的是 ( )
时,下列式子大小关系正确的是 ( )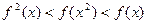
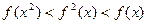
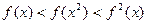
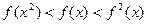
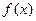 满足
满足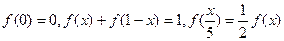 ,且当
,且当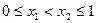 时,
时,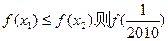 等于 ( )
等于 ( )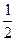
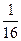
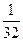
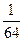
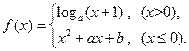 若
若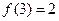 ,
,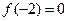 ,则
,则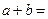

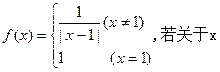 的方程
的方程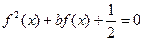 有5个不同的根
有5个不同的根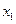 、
、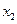 、
、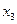 、
、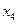 、
、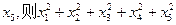 等于 。
等于 。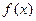 的定义域为
的定义域为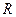 ,若存在常数
,若存在常数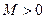 ,使
,使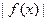 ≤
≤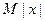 对一切实数
对一切实数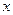 均成立,则称
均成立,则称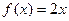 ;
;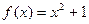 ;
;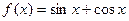 ;
;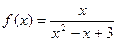 ;
;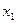 ,
,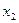 均有
均有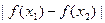 ≤
≤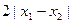 .其中是“倍约束函数”的有 ( )
.其中是“倍约束函数”的有 ( )
