题目内容
【题目】已知直线
与双曲线
；
（1）当
为何值时，直线与双曲线有一个交点；
（2）直线与双曲线交于
、
两点且以
为直径的圆过坐标原点，求值。
【答案】（1）当
或
时，直线与双曲线有一个交点（2）
【解析】
（1）根据直线与双曲线的位置关系中直线与双曲线有一个交点的情况，讨论直线与双曲线的渐近线平行与不平行，解出即可得到答案。
（2）联立直线与双曲线可得到
，
，直线与双曲线交于
、
两点且以
为直径的圆过坐标原点等价于
，即
，代入即可解出答案。
（1）直线
过定点
，双曲线
渐近线方程为
，
①当直线与双曲线的渐近线平行时，只有一个交点，此时；
②当
时，联立与得：
，
若直线与双曲线只有一个交点，则
，解得，
所以，当或时，直线与双曲线有一个交点；
（2）设点
，
，
联立与得：，
所以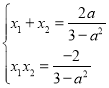
，
，
因为以为直径的圆过坐标原点，所以，
所以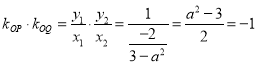
，
解得.满足判别式大于0
练习册系列答案
相关题目
【题目】据统计ABO血型具有民族和地区差异.在我国H省调查了30488人，四种血型的人数如下：
血型 | A | B | O | AB |
人数/人 | 7704 | 10765 | 8970 | 3049 |
频率 |
（1）计算H省各种血型的频率并填表（精确到0.001）；
（2）如果从H省任意调查一个人的血型，那么他是O型血的概率大约是多少？
