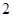题目内容
(本小题满分12分)
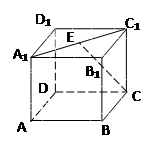
如图,三棱柱ABC—A1B1C1中,底面为正三角形,侧棱与底面垂直,D是BC的中点,AA1=AB=1。

(1) 求证:A1C∥平面AB1D;
(2) 求点C到平面AB1D的距离。
如图,三棱柱ABC—A1B1C1中,底面为正三角形,侧棱与底面垂直,D是BC的中点,AA1=AB=1。

(1) 求证:A1C∥平面AB1D;
(2) 求点C到平面AB1D的距离。
(1)见解析;(2)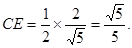
本试题主要是考查了线面平行的判定和点到面的距离的求解的综合运用。
(1)由于连接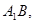 交
交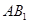 与点O,则O是
与点O,则O是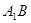 的中点,又
的中点,又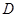 是
是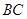 中点,
中点,
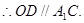 ,则由判定定理得到结论。
,则由判定定理得到结论。
(2)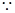 正三角形ABC,
正三角形ABC,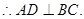
又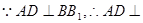 面
面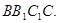 ,然后利用面面垂直的性质定理得到点到面的距离的表示,进而求解。
,然后利用面面垂直的性质定理得到点到面的距离的表示,进而求解。
(1)连接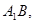 交
交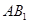 与点O,则O是
与点O,则O是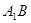 的中点,又
的中点,又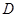 是
是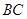 中点,
中点,
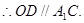 又
又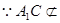 面
面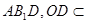 面
面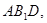
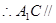 面
面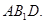
(2)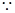 正三角形ABC,
正三角形ABC,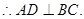
又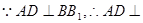 面
面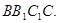
在面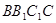 内作
内作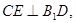 则
则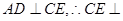 面
面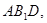
(1)由于连接
 交
交 与点O,则O是
与点O,则O是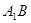 的中点,又
的中点,又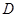 是
是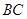 中点,
中点,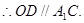 ,则由判定定理得到结论。
,则由判定定理得到结论。(2)
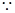 正三角形ABC,
正三角形ABC,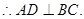
又
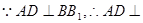 面
面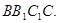 ,然后利用面面垂直的性质定理得到点到面的距离的表示,进而求解。
,然后利用面面垂直的性质定理得到点到面的距离的表示,进而求解。(1)连接
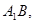 交
交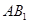 与点O,则O是
与点O,则O是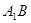 的中点,又
的中点,又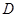 是
是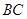 中点,
中点,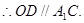 又
又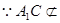 面
面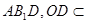 面
面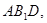
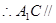 面
面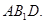
(2)
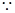 正三角形ABC,
正三角形ABC,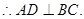
又
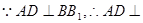 面
面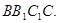
在面
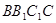 内作
内作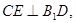 则
则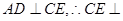 面
面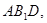
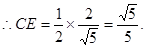

练习册系列答案
相关题目
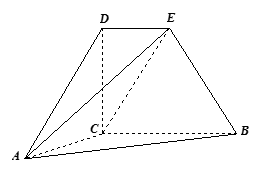
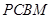 是直角梯形,
是直角梯形,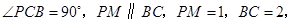 又
又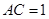 ,
,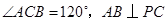 ,直线
,直线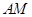 与直线
与直线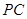 所成的角为
所成的角为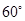 .
.
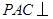 平面
平面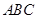 ;
;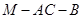 的大小;
的大小;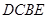 为直角梯形,
为直角梯形,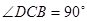 ,
,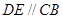 ,
,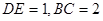 ,又
,又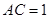 ,
,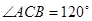 ,
,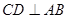 ,直线
,直线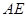 与直线
与直线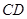 所成角为
所成角为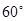 .
.
 平面
平面 ;
; 与平面
与平面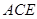 所成角的正弦值.
所成角的正弦值.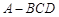 中,
中, 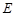 是
是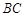 的中点,
的中点,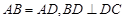
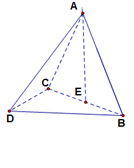
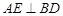 ;
;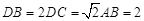 ,且二面角
,且二面角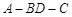 为
为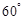 ,求
,求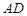 与面
与面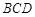 所成角的正弦值。
所成角的正弦值。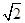 .
.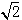 ,PD⊥BC。
,PD⊥BC。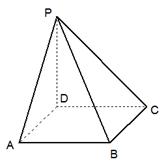
 中,底面ABCD为直角梯形,AB∥CD,∠BAD=90°,PA⊥平面ABCD,AB=1,AD=2,PA=CD=4,求二面角
中,底面ABCD为直角梯形,AB∥CD,∠BAD=90°,PA⊥平面ABCD,AB=1,AD=2,PA=CD=4,求二面角 的余弦值.
的余弦值.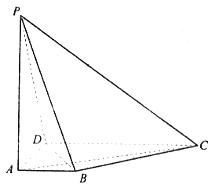

 的底面边长为
的底面边长为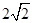 ,
,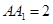 ,点
,点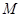 是
是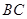 的中点,
的中点,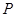 是平面
是平面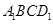 内的一个动点,且满足
内的一个动点,且满足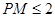 ,
,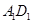 和
和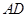 的距离相等,则点
的距离相等,则点