��Ŀ����
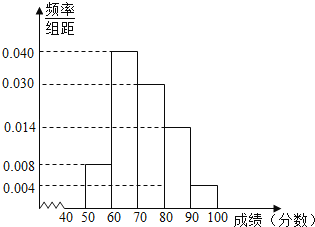
����Ŀ��ѧУ�ӲμӸ߶��꼶��ĩ���Ե�ѧ���г��һЩѧ������ͳ�������ǵ���ѧ�ɼ����ɼ���Ϊ����������Ϊ100�֣������������������г�������Ƶ�ʷֲ�����
���� | Ƶ�� | Ƶ�� |
[40��50�� | A | 0.04 |
[50��60�� | 4 | 0.08 |
[60��70�� | 20 | 0.40 |
[70��80�� | 15 | 0.30 |
[80��90�� | 7 | B |
[90��100] | 2 | 0.04 |
�ϼ� | C | 1 |
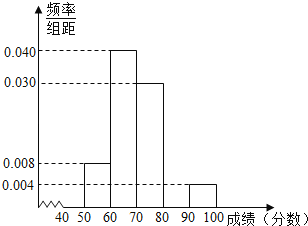
��1���ڸ���������Ƶ�ʷֲ����У���A��B��C��ֵ��
��2����ȫƵ�ʷֲ�ֱ��ͼ��������������ȫ��߶��꼶ѧ����ĩ��ѧ�ɼ�����������λ����
��3���ִӷ�����[80��90����[90��100]��9��ͬѧ�������ȡ����ͬѧ����ȡ������ѧ��������������90�ֵĸ��ʣ�
���𰸡���1��2��0.14��50��2��65�� 69.5��3��![]() ��
��
��������
(1)����Ƶ�ʷֲ���,���Ƶ��,ֱ�����![]() ,
,![]() ,
,![]() ��ֵ;
��ֵ;
(2)�������,��λ��,����Ƶ�ʷֲ�ֱ��ͼ����;
(3)���ùŵ�����ʵ���,�����ʼ���.
(1)![]() ;
;
(2)����Ϊ��ߵ�С���������е�65,
��λ��Ϊ![]() ,
,
Ƶ��ֱ��ͼ����:
(3)����={�ӷ�����[80,100]��10��ͬѧ�������ȡ����ͬѧ},
![]() ,
,
A={����ѧ��������������90��},n(A)=1,
���ݹŵ���ͼ��㹫ʽ�ɵ�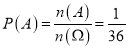 .
.

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ