题目内容
10．若a=${∫}_{0}^{π}$sinxdx，则（x+$\frac{1}{x}$）（ax-1）5的展开式中的常数项为（ ）| A． | 10 | B． | 20 | C． | -10 | D． | -20 |
分析 求定积分可得a的值，把（2x-1）5按照二项式定理展开，即可求得（x+$\frac{1}{x}$）（2x-1）5展开式的常数项．
解答 解：a=${∫}_{0}^{π}$sinxdx=-cosx${|}_{0}^{π}$=2，
则（x+$\frac{1}{x}$）（ax-1）5=（x+$\frac{1}{x}$）（2x-1）5 =（x+$\frac{1}{x}$）（32x5-80x4+80x3-40x2+10x-1），
故（x+$\frac{1}{x}$）（2x-1）5展开式的常数项为$\frac{1}{x}•（10x）$=10，
故选：A．
点评 本题主要考查求定积分，二项式定理的应用，求展开式中某项的系数，二项式系数的性质，属于基础题．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
相关题目
20．在△ABC中，cosA=$\frac{4}{5}$，cosB=$\frac{12}{13}$，则sinC=（ ）
| A． | $\frac{33}{65}$ | B． | $\frac{56}{65}$ | C． | -$\frac{33}{65}$ | D． | -$\frac{56}{65}$ |
18．某工厂对同时生产某件产品的件数x（单位：件）与所用时间y（单位：小时）进行了测验．测验结果如下表所示：
（1）求出y与x的线性回归方程$\widehat{y}$=bx+a；
（2）试预测同时生产20件该产品需要多少小时？
（附：线性回归方程$\widehat{y}$=bx+a中，b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}-b\overline{x}$）
| 件数x（件） | 11 | 12 | 13 |
| 时间y（小时） | 25 | 26 | 30 |
（2）试预测同时生产20件该产品需要多少小时？
（附：线性回归方程$\widehat{y}$=bx+a中，b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}-b\overline{x}$）
5．已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的两焦点分别是F1，F2，过F1的直线交椭圆于P，Q两点，若|PF2|=|F1F2|，且2|PF1|=3|QF1|，则椭圆的离心率为（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{3\sqrt{2}}{5}$ |
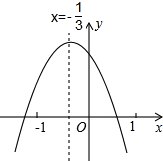已知二次函数y=ax2+bx+c的图象如图，对称轴是直线x=-$\frac{1}{3}$，下列结论：①ab＞0；②a+b+c＜0；③b+2c＜0；④a-2b+4c＞0．其中正确结论的个数是（ ）
如图，已知椭圆C的中心在原点，焦点 F1，F2在x轴上，焦距与短轴长均为2$\sqrt{2}$．