题目内容
10.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+\frac{5}{2}x-1,x<0}\\{{e}^{x},x≥0}\end{array}\right.$,若|f(x)|≥ax+1,则实数a的取值范围是$[-\frac{5}{2},1]$.分析 由f(x)解析式化简|f(x)|,根据x的范围分别化简|f(x)|≥ax+1,利用分离常数法和函数图象的切线求出实数a的取值范围.
解答 解:由题意得,f(x)=$\left\{\begin{array}{l}{-{x}^{2}+\frac{5}{2}x-1,x<0}\\{{e}^{x},x≥0}\end{array}\right.$,
则|f(x)|=$\left\{\begin{array}{l}{{x}^{2}-\frac{5}{2}x+1,x<0}\\{{e}^{x},x≥0}\end{array}\right.$,
当x<0时,不等式|f(x)|≥ax+1为:${x}^{2}-\frac{5}{2}x+1≥ax+1$,
所以a≥x-$\frac{5}{2}$在(-∞,0)上恒成立,则a≥-$\frac{5}{2}$;
当x≥0时,不等式|f(x)|≥ax+1为:ex≥ax+1,
①当a≤0时,不等式ex≥ax+1恒成立,
②当a>0时,函数y=ex在(0,1)处的切线方程是y=x+1,
所以不等式ex≥ax+1恒成立需要:a≤1,
则a的取值范围是(-∞,1],
综上可得,a的取值范围是$[-\frac{5}{2},1]$,
故答案为:$[-\frac{5}{2},1]$.
点评 本题以分段函数为载体考查恒成立问题,考查分离常数法,函数图象的切线,以及转化思想,属于中档题.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
15.已知函数f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$,x∈R,若对任意θ∈(0,$\frac{π}{2}$],都有f(msinθ)+f(1-m)>0成立,则实数m的取值范围( )
| A. | (0,1) | B. | (0,2) | C. | (-∞,1) | D. | (-∞,1] |
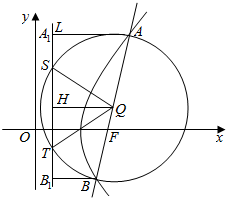 以圆锥曲线的焦点弦AB为直径作圆,与相应准线l有两个不同的交点,求证:
以圆锥曲线的焦点弦AB为直径作圆,与相应准线l有两个不同的交点,求证: