Question

1．已知函数f（x）=|xlnx|．方程f²（x）-（2+e）f（x）+2e=0的实根个数为（　　）

• A． 2
• B． 4
• C． 5
• D． 6

Answer 1

分析 求导得到f（x）=|xlnx|的取值情况，画出草图，令t=f（x）=|xlnx|．则方程f²（x）-（2+e）f（x）+2e=0化为t²-（2+e）t+2e=0．解方程求出t的值，数形结合求得方程f²（x）-（2+e）f（x）+2e=0的实根个数．

解答 解：令g（x）=xlnx，则g′（x）=lnx+1，
由g′（x）=lnx+1=0，得$x=\frac{1}{e}$．
当x∈（0，$\frac{1}{e}$）时，g′（x）＜0；当x∈（$\frac{1}{e}$，+∞）时，g′（x）＞0．
∴g（x）在（0，$\frac{1}{e}$）上为减函数，在（$\frac{1}{e}$，+∞）上为增函数．
∴$g（x）_{min}=g（\frac{1}{e}）=-\frac{1}{e}$．
令t=f（x）=|xlnx|．
作出函数t=|xlnx|的草图如图：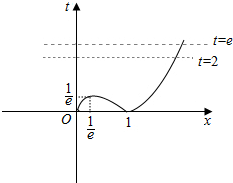

由f²（x）-（2+e）f（x）+2e=0，即t²-（2+e）t+2e=0．
解得：t=2或t=e．
结合上图可知，方程f²（x）-（2+e）f（x）+2e=0的实根个数为2．
故选：A．

点评 本题考查根的存在性及根的个数判断，考查了数形结合的解题思想方法，考查了换元法，是中档题．