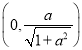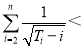题目内容
【题目】在平面直角坐标系xOy中,已知椭圆![]() 经过
经过![]() ,且右焦点坐标为
,且右焦点坐标为![]() .
.
(1)求椭圆的标准方程;
(2)设A,B为椭圆的左,右顶点,C为椭圆的上顶点,P为椭圆上任意一点(异于A,B两点),直线AC与直线BP相交于点M,直线BC与直线AP相交于点N,求证:![]() .
.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)由椭圆的定义,可得![]() ,又
,又![]() ,结合
,结合![]() ,即得解
,即得解
(2)设![]() ,分别表示直线
,分别表示直线![]() 的方程,联立得到
的方程,联立得到![]() 点的坐标,继而证明
点的坐标,继而证明![]() ,即直线
,即直线![]() 斜率不存在,
斜率不存在,![]() ,即
,即![]() ,可得
,可得![]() 为等腰三角形,即得证
为等腰三角形,即得证
(1)由题意,椭圆的两个焦点坐标为![]() ,记
,记![]()
故![]()
又![]()
故椭圆的方程为:![]()
(2)设![]() ,
,![]()
故:![]()
![]()
![]()
联立计算可得:

由于![]()
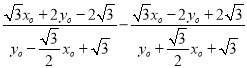
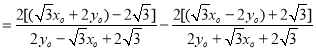
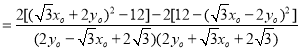
![]()
由于![]() 在椭圆上,故
在椭圆上,故![]() ,即
,即![]()
故![]() ,即直线
,即直线![]() 斜率不存在
斜率不存在
令线段![]() 中点为
中点为![]()
故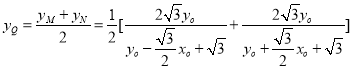
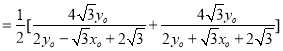

故![]()
![]()
故![]() 为等腰三角形
为等腰三角形
即得证 ![]()

练习册系列答案
相关题目