题目内容
已知函数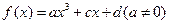 是
是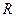 上的奇函数,当
上的奇函数,当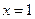 时
时 取得极值
取得极值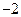 .
.
(1)求 的单调区间和极大值;
的单调区间和极大值;
(2)证明对任意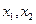
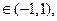 不等式
不等式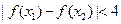 恒成立.
恒成立.
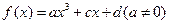 是
是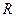 上的奇函数,当
上的奇函数,当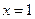 时
时 取得极值
取得极值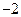 .
.(1)求
 的单调区间和极大值;
的单调区间和极大值;(2)证明对任意
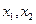
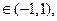 不等式
不等式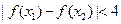 恒成立.
恒成立.(1) 在单调区间
在单调区间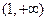 ,
,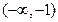 上是增函数,
上是增函数, 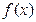 在单调区间
在单调区间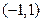 上是减函数,
上是减函数, 在
在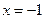 处取得极大值,极大值为
处取得极大值,极大值为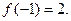 (2)证明略
(2)证明略
 在单调区间
在单调区间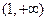 ,
,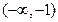 上是增函数,
上是增函数, 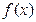 在单调区间
在单调区间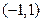 上是减函数,
上是减函数, 在
在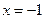 处取得极大值,极大值为
处取得极大值,极大值为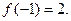 (2)证明略
(2)证明略(1)由奇函数定义,有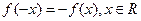 . 即
. 即 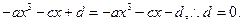 因此,
因此,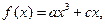
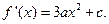
由条件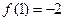 为
为 的极值,必有
的极值,必有
故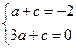 ,解得
,解得 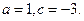
因此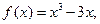
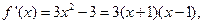
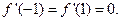
当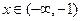 时,
时,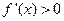 ,故
,故 在单调区间
在单调区间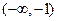 上是增函数.
上是增函数.
当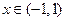 时,
时,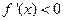 ,故
,故 在单调区间
在单调区间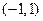 上是减函数.
上是减函数.
当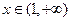 时,
时,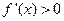 ,故
,故 在单调区间
在单调区间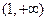 上是增函数.
上是增函数.
所以, 在
在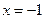 处取得极大值,极大值为
处取得极大值,极大值为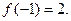
(2)由(1)知,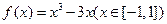 是减函数,且
是减函数,且
 在
在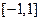 上的最大值为
上的最大值为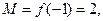 最小值为
最小值为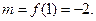
所以,对任意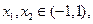 恒有
恒有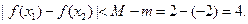
[方法技巧]善于用函数思想不等式问题,如本题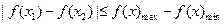 .
.
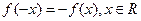 . 即
. 即 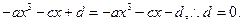 因此,
因此,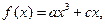
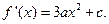
由条件
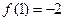 为
为 的极值,必有
的极值,必有
故
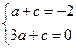 ,解得
,解得 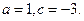
因此
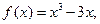
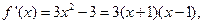
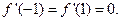
当
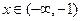 时,
时,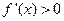 ,故
,故 在单调区间
在单调区间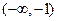 上是增函数.
上是增函数.当
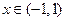 时,
时,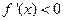 ,故
,故 在单调区间
在单调区间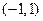 上是减函数.
上是减函数.当
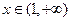 时,
时,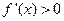 ,故
,故 在单调区间
在单调区间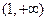 上是增函数.
上是增函数.所以,
 在
在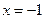 处取得极大值,极大值为
处取得极大值,极大值为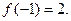
(2)由(1)知,
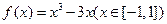 是减函数,且
是减函数,且 在
在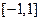 上的最大值为
上的最大值为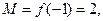 最小值为
最小值为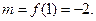
所以,对任意
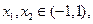 恒有
恒有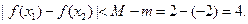
[方法技巧]善于用函数思想不等式问题,如本题
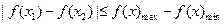 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
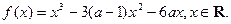
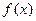 的单调区间; (II)当
的单调区间; (II)当 在区间[—1,2]上是单调函数,求a的取值范围。
在区间[—1,2]上是单调函数,求a的取值范围。 上求一点P,当△PAB面积最大时,P点坐标为 .
上求一点P,当△PAB面积最大时,P点坐标为 .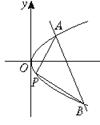
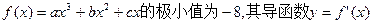
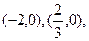 如图所示, (Ⅰ)求
如图所示, (Ⅰ)求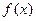 的解析式;
的解析式;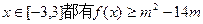 恒成立,
恒成立,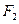 为圆心,过另一焦点
为圆心,过另一焦点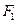 的圆被右准线截的两段弧长之比2:1,
的圆被右准线截的两段弧长之比2:1,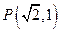 为此平面上一定点,且
为此平面上一定点,且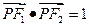 .(1)求椭圆的方程(2)若直线
.(1)求椭圆的方程(2)若直线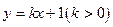 与椭圆交于如图两点A、B,令
与椭圆交于如图两点A、B,令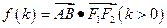 。求函数
。求函数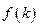 的值域
的值域