题目内容
【题目】已知函数![]() 的图象上的一个最低点为
的图象上的一个最低点为![]() ,周期为
,周期为![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)将![]() 的图象上的所有点的横坐标伸长到原来的2倍(纵坐标不变),然后再将所得的图象沿
的图象上的所有点的横坐标伸长到原来的2倍(纵坐标不变),然后再将所得的图象沿![]() 轴向右平移
轴向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,写出函数
的图象,写出函数![]() 的解析式;
的解析式;
(3)当![]() 时,求函数
时,求函数![]() 的最大值和最小值.
的最大值和最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)依题意,可求得![]() ,
,![]() ,
,![]() ,再由
,再由![]() ,
,![]() ,
,![]() ,可求得
,可求得![]() 于是可求得
于是可求得![]() 的解析式;
的解析式;
(2)根据三角函数的变换规则计算可得;
(3)由![]() 的取值范围,求出
的取值范围,求出![]() 的范围,结合正弦函数的性质计算可得;
的范围,结合正弦函数的性质计算可得;
解:(1)由题意得,![]() ,
,
![]() ,
,![]() ,
,
![]() ,又
,又![]()
所以![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
(2)将![]() 的图象上的所有点的横坐标伸长到原来的2倍(纵坐标不变),得到
的图象上的所有点的横坐标伸长到原来的2倍(纵坐标不变),得到![]()
再将所得的图象沿![]() 轴向右平移
轴向右平移![]() 个单位,得到函数
个单位,得到函数![]()
即![]()
(3)因为![]() ,所以
,所以![]() ,所以
,所以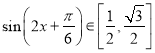 ,所以
,所以![]() ,即
,即![]() ,
,![]()

【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/℃ | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2) 若由线性回归方程得到的估计数据与4月份所选5天的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的. 请根据4月7日,4月15日与4月21日这三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判定所得的线性回归方程是否可靠?
,并判定所得的线性回归方程是否可靠?
参考公式: 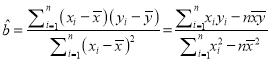 ,
, ![]()
参考数据: ![]()
【题目】以下表格记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以![]() 表示.
表示.
甲组 | 9 | 9 | 11 | 11 |
乙组 |
| 8 | 9 | 10 |
(1)如果![]() ,求乙组同学植树棵数的平均数和方差;
,求乙组同学植树棵数的平均数和方差;
(2)如果![]() ,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
