题目内容
【题目】以下表格记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊，无法确认，在图中以
表示.
甲组 | 9 | 9 | 11 | 11 |
乙组 |
| 8 | 9 | 10 |
（1）如果
，求乙组同学植树棵数的平均数和方差；
（2）如果
，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率.
【答案】（1）平均数
；方差
；（2）
【解析】
（1）利用平均数和方差的定义，即可得解；
（2）列举出基本事件个数和符合条件的基本事件个数，用古典概型概率公式即可求得概率.
（1）当
时，乙组同学的植树棵数是8，8，9，10，
所以，乙组同学植树棵数的平均数
，
乙组同学植树棵数的方差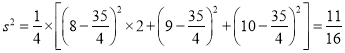
.
（2）当
时，甲组同学的植树棵树是：9，9，11，11，
乙组同学的植树棵数是：9，8，9，10.
分别从甲、乙两组中随机选取一名同学，所有可能的结果为：
，
，，
，，，，，
，
，，
，，，，，共16种，
这两名同学的植树总棵数为19的情况为：，，，，共4种，
所以，这两名同学的植树总棵数为19的概率
.
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关，通过随机调查200名高中生是否爱好某项运动，利用
列联表，由计算可得
，参照下表：
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是（ ）
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别无关”
