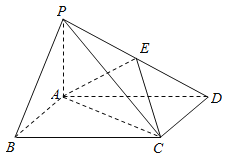
题目内容
【题目】已知等差数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,公差为
,公差为![]()
![]() 若
若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
![]() 是否存在d,n使
是否存在d,n使![]() 成立?若存在,试找出所有满足条件的d,n的值,并求出数列
成立?若存在,试找出所有满足条件的d,n的值,并求出数列![]() 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
![]() 由已知求得公差,直接代入等差数列的通项公式得答案;
由已知求得公差,直接代入等差数列的通项公式得答案;![]() 由
由![]() ,得到
,得到![]() ,然后依次取n值,求得d,分类分析即可得到所有满足条件的d,n的值,并求得通项公式.
,然后依次取n值,求得d,分类分析即可得到所有满足条件的d,n的值,并求得通项公式.
![]() 当
当![]() 时,由
时,由![]() ,得
,得![]() ,即
,即![]() .
.
![]() ;
;
![]() 由题意可知,
由题意可知,![]() ,
,
即![]() ,
,![]() .
.
令![]() 时,得
时,得![]() ,不合题意;
,不合题意;
![]() 时,得
时,得![]() ,符合.
,符合.
此时数列的通项公式为![]() ;
;
![]() 时,得
时,得![]() ,不合题意;
,不合题意;
![]() 时,得
时,得![]() ,符合.
,符合.
此时数列的通项公式为![]() ;
;
![]() 时,得
时,得![]() ,符合.
,符合.
此时数列的通项公式为![]() ;
;
![]() 时,得
时,得![]() ,不合题意;
,不合题意;
![]() 时,得
时,得![]() ,不合题意;
,不合题意;
![]() 时,得
时,得![]() ,不合题意;
,不合题意;
![]() 时,
时,![]() ,均不合题意.
,均不合题意.
![]() 存在3组,其解与相应的通项公式分别为:
存在3组,其解与相应的通项公式分别为:
![]() ,
,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() .
.

【题目】某校在高二年级学生中,对自然科学类、社会科学类校本选修课程的选课意向进行调查.现从高二年级学生中随机抽取180名学生,其中男生105名;在这180名学生中选择社会科学类的男生、女生均为45名.
(1)根据抽取的180名学生的调查结果,完成下面的2×2列联表.
(2)判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关?
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 | |||
合计 |
参考公式:![]() ,其中
,其中![]() .
.
P(K2≥k0) | 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 | |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】随着西部大开发的深入,西南地区的大学越来越受到广大考生的青睐,下表是西南地区某大学近五年的录取平均分高于省一本线分值对比表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
录取平均分高于省一本线分值 | 28 | 34 | 41 | 47 | 50 |
(1)根据上表数据可知,![]() 与
与![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)假设2020年该省一本线为520分,利用(1)中求出的回归方程预测2020年该大学录取平均分.
参考公式: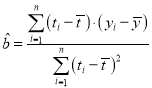 ,
,![]()