题目内容
(本小题满分15分)
已知函数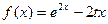 ,
,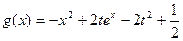 。
。
(Ⅰ)求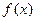 在区间
在区间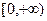 的最小值;
的最小值;
(Ⅱ)求证:若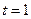 ,则不等式
,则不等式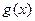 ≥
≥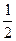 对于任意的
对于任意的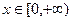 恒成立;
恒成立;
(Ⅲ)求证:若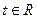 ,则不等式
,则不等式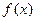 ≥
≥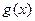 对于任意
对于任意 的
的
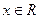 恒成立。
恒成立。
已知函数
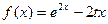 ,
,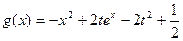 。
。(Ⅰ)求
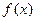 在区间
在区间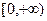 的最小值;
的最小值;(Ⅱ)求证:若
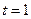 ,则不等式
,则不等式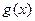 ≥
≥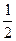 对于任意的
对于任意的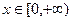 恒成立;
恒成立;(Ⅲ)求证:若
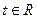 ,则不等式
,则不等式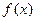 ≥
≥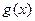 对于任意
对于任意 的
的
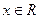 恒成立。
恒成立。解(Ⅰ): ………………………………………1分
………………………………………1分
①若
∵ ,则
,则 ,∴
,∴ ,即
,即 。
。
∴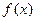 在区间
在区间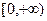 是增函数,故
是增函数,故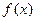 在区间
在区间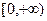 的最小值是
的最小值是 。……3分
。……3分
②若
令 ,得
,得 .
.
又当 时,
时, ;当
;当 时,
时, ,
,
∴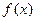 在区间
在区间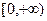 的最小值是
的最小值是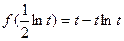 ………………………………5分
………………………………5分
综上,当 时,
时,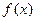 在区间
在区间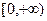 的最小值是
的最小值是 ,当
,当 时,
时,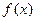 在区间
在区间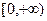 的最小值是
的最小值是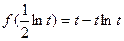 。……………………………………………6分
。……………………………………………6分
(Ⅱ)证明:当 时,
时, ,则
,则 ,7分
,7分
∴ ,
,
当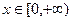 时,有
时,有 ,∴
,∴ 在
在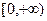 内是增函数,
内是增函数,
∴ ,
,
∴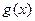 在
在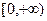 内是增函数,
内是增函数,
∴对于任意的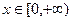 ,
, 恒成立。…………………………………1
恒成立。…………………………………1 0分
0分
(Ⅲ)证明:
 ,
,
令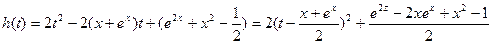
则当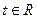 时,
时, ≥
≥
 ,……………………………………………12分
,……………………………………………12分
令 ,则
,则 ,
,
当
 时,
时,  ;当
;当 时,
时, ;当
;当 时,
时, ,
,
则 在
在 是减函数,在
是减函数,在 是增函数,
是增函数,
∴ ,∴
,∴ ,
,
∴ ,即不等式
,即不等式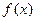 ≥
≥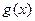 对于任意的
对于任意的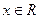 恒成立。……………15分
恒成立。……………15分
 ………………………………………1分
………………………………………1分①若

∵
 ,则
,则 ,∴
,∴ ,即
,即 。
。∴
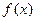 在区间
在区间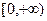 是增函数,故
是增函数,故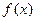 在区间
在区间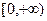 的最小值是
的最小值是 。……3分
。……3分②若

令
 ,得
,得 .
.又当
 时,
时, ;当
;当 时,
时, ,
,∴
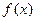 在区间
在区间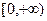 的最小值是
的最小值是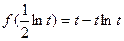 ………………………………5分
………………………………5分综上,当
 时,
时,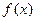 在区间
在区间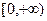 的最小值是
的最小值是 ,当
,当 时,
时,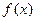 在区间
在区间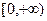 的最小值是
的最小值是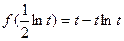 。……………………………………………6分
。……………………………………………6分(Ⅱ)证明:当
 时,
时, ,则
,则 ,7分
,7分∴
 ,
,当
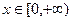 时,有
时,有 ,∴
,∴ 在
在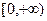 内是增函数,
内是增函数,∴
 ,
,∴
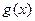 在
在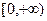 内是增函数,
内是增函数,∴对于任意的
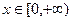 ,
, 恒成立。…………………………………1
恒成立。…………………………………1 0分
0分(Ⅲ)证明:

 ,
,令
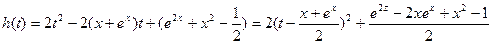
则当
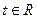 时,
时, ≥
≥
 ,……………………………………………12分
,……………………………………………12分令
 ,则
,则 ,
,当

 时,
时,  ;当
;当 时,
时, ;当
;当 时,
时, ,
,则
 在
在 是减函数,在
是减函数,在 是增函数,
是增函数,∴
 ,∴
,∴ ,
,∴
 ,即不等式
,即不等式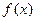 ≥
≥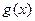 对于任意的
对于任意的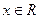 恒成立。……………15分
恒成立。……………15分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
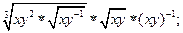
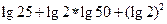 的值。
的值。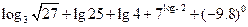 ;
; 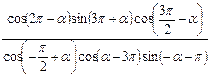 。
。 象限.
象限.
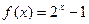 的反函数为
的反函数为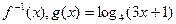
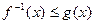 ,求
,求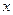 的取值范围D;
的取值范围D;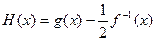 ;当
;当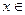 D时,求函数H
D时,求函数H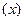 的值域
的值域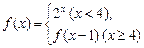 ,则
,则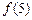 =_______
=_______

 ,
, ,
, 按从小到大的顺序排列是 < < 。
按从小到大的顺序排列是 < < 。