题目内容
1.已知a为正实数,函数f(x)=x2-2x+a,且对任意的x∈[0,a],都有f(x)∈[-a,a],则实数a的取值范围是(0,2].分析 先求出函数的对称轴,通过讨论a的范围,得到函数的单调性,表示出f(x)的最值,从而求出a的范围即可.
解答 解:f(x)=(x-1)2+a-1,对称轴x=1,
①0<a≤1时,f(x)在[0,a]递减,
f(x)max=f(0)=a,f(x)min=f(a)=a2-a,
即函数的值域为[a2-a,a]⊆[-a,a],
∴-a≤a2-a,解得:a∈(0,1];
②当a∈(1,2]时:f(x)max=f(0)=a,f(x)min=f(1)=a-1,
即函数的值域是[a-1,a]⊆[-a,a],
∴-a≤a-1,解得:a∈(1,2];
③当a∈(2,+∞)时:f(x)max=f(a)=a2-a,f(x)min=f(1)=a-1,
即函数的值域是[a-1,a2-a]⊆[-a,a],
∴a2-a≤a,解得:a∈∅,
综上:a∈(0,2].
点评 本题考查了二次函数的性质,考查函数的单调性、最值问题,是一道中档题.

练习册系列答案
相关题目
13.下列结论中正确的是( )
| A. | 如果直线l垂直于平面α内的无数条直线,那么l⊥α | |
| B. | 如果直线1平行于平面α内的无数条直线,那么l∥α | |
| C. | 过空间一点有且只有一条直线平行于已知平面 | |
| D. | 过空间一点有且只有一条直线垂直于已知平面 |
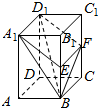 长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E、F分别为侧棱BB1、CC1的中点,求四棱锥B-A1EFD1的体积.
长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E、F分别为侧棱BB1、CC1的中点,求四棱锥B-A1EFD1的体积.