题目内容
12.(1)证明不等式$\frac{x}{1+x}$<ln(1+x)<x,x>0(2)在数列{an}中.已知a1=$\frac{1}{2}$,且$\frac{{a}_{n}{a}_{n-1}}{{a}_{n-1}-{a}_{n}}$=1+$\frac{1}{{n}^{2}-n-1}$,求数列{an}的通项公式an.
分析 (1)设$ϕ(x)=ln(x+1)-\frac{x}{1+x},x∈[0,+∞)$,得:$ϕ'(x)=\frac{1}{x+1}-\frac{1}{{{{(1+x)}^2}}}=\frac{x}{{{{(1+x)}^2}}}$,由此能够证明$\frac{x}{1+x}<ln(x+1)$<x.
(2)利用取倒数法,以及累加法进行求解即可.
解答 解:(1)设$ϕ(x)=ln(x+1)-\frac{x}{1+x},x∈[0,+∞)$
对ϕ(x)求导,得:$ϕ'(x)=\frac{1}{x+1}-\frac{1}{{{{(1+x)}^2}}}=\frac{x}{{{{(1+x)}^2}}}$
当x>0时,ϕ′(x)>0,
∴ϕ(x)在(0,+∞)内是增函数.
当x>0时,ϕ(x)>ϕ(0)=0,
即$ln(x+1)-\frac{x}{1+x}>0$,
∴$\frac{x}{1+x}<ln(x+1)$
同理可证ln(x+1)<x,
∴$\frac{x}{1+x}<ln(x+1)$<x.
(2)$\frac{{a}_{n}{a}_{n-1}}{{a}_{n-1}-{a}_{n}}$=1+$\frac{1}{{n}^{2}-n-1}$=$\frac{{n}^{2}-n-1+1}{{n}^{2}-n-1}$=$\frac{{n}^{2}-n}{{n}^{2}-n-1}$,
等式两边取倒数得$\frac{{a}_{n-1}-{a}_{n}}{{a}_{n}{a}_{n-1}}$=$\frac{{n}^{2}-n-1}{{n}^{2}-n}$,
即$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=1-$\frac{1}{{n}^{2}-n}$=1-$\frac{1}{n(n-1)}$=1-($\frac{1}{n-1}$-$\frac{1}{n}$)=1-$\frac{1}{n-1}$+$\frac{1}{n}$,
则当n≥2时,$\frac{1}{{a}_{2}}$-$\frac{1}{{a}_{1}}$=1-1+$\frac{1}{2}$,
$\frac{1}{{a}_{3}}$-$\frac{1}{{a}_{2}}$=1-$\frac{1}{2}$+$\frac{1}{3}$,
$\frac{1}{{a}_{4}}$-$\frac{1}{{a}_{3}}$=1-$\frac{1}{3}$+$\frac{1}{4}$,
…
$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=1-$\frac{1}{n-1}$+$\frac{1}{n}$,
等式两边同时相加得
$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{1}}$=n-1-1+$\frac{1}{n}$=n-1+$\frac{1}{n}$,
即$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{1}}$+n-1+$\frac{1}{n}$=2+n-1+$\frac{1}{n}$=n+1+$\frac{1}{n}$=$\frac{{n}^{2}+n+1}{n}$,
即an=$\frac{n}{{n}^{2}+n+1}$,
当n=1时,a1=$\frac{1}{2}$不满足an=$\frac{n}{{n}^{2}+n+1}$,
故an=$\left\{\begin{array}{l}{\frac{1}{2},}&{n=1}\\{\frac{n}{{n}^{2}+n+1},}&{n≥2}\end{array}\right.$.
点评 本题考查函数的单调区间的求法,考查不等式的证明,考查推理论证能力,考查运算推导能力,考查等价转化思想,解题时要认真审题,仔细解答,注意导数性质的综合应用.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案 如图,在复平面内,若复数z1,z2对应的向量分别是$\overrightarrow{{O}{A}}$,$\overrightarrow{{O}{B}}$,则复数z=z1z2-z1-z2-i所对应的点位于( )
如图,在复平面内,若复数z1,z2对应的向量分别是$\overrightarrow{{O}{A}}$,$\overrightarrow{{O}{B}}$,则复数z=z1z2-z1-z2-i所对应的点位于( )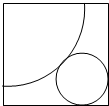 如图,在边长为5+$\sqrt{2}$的正方形纸片中剪下如图所示的扇形和圆,使它恰好成同一圆锥的侧面和底面,求此圆锥的体积.
如图,在边长为5+$\sqrt{2}$的正方形纸片中剪下如图所示的扇形和圆,使它恰好成同一圆锥的侧面和底面,求此圆锥的体积.