题目内容
1.已知曲线C1:ρ=2cosθ,曲线C2:$\left\{\begin{array}{l}{x=5cost}\\{y=4sint}\end{array}\right.$(t为参数),(1)化C1为直角坐标方程,化C2为普通方程;
(2)若M为曲线C2上一动点,N为曲线C1上一动点,求|MN|的取值范围.
分析 (1)直接根据极坐标和直角坐标互化公式求解即可;
(2)利用已知,得到|MC2|-1≤|MN|≤|MC2|+1,然后,得到|MC2|2=(5cosφ-1)2+16sin2φ=9cos2φ-10cosφ+17,借助于三角函数的取值情况进行求解即可.
解答 解:(1)∵曲线C1:ρ=2cosθ,
∴ρ2=2ρcosθ,
∴x2+y2=2x,
故它的直角坐标方程为x2+y2-2x=0,
即:C1:(x-1)2+y2=1,
∵曲线C2:$\left\{\begin{array}{l}{x=5cost}\\{y=4sint}\end{array}\right.$(t为参数),
∴$\left\{\begin{array}{l}{cost=\frac{x}{5}}\\{sint=\frac{y}{4}}\end{array}\right.$(t为参数),
∴平方相加后可得:C2:$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1.
(2)设点M(5cost,4sint),则
|MC2|-1≤|MN|≤|MC2|+1,
|MC2|2=(5cost-1)2+16sin2t=9cos2t-10cost+17=9(cost-$\frac{5}{9}$)2+$\frac{128}{9}$,
当cost=-1时,得|MC2|2max=36,|MC2|max=6,
当cost=$\frac{5}{9}$时,得|MC2|2min=$\frac{128}{9}$,|MC2|min=$\frac{8\sqrt{2}}{3}$,
∴$\frac{8\sqrt{2}}{3}$-1≤|MC2|-1≤|MN|≤|MC2|+1≤5+1,
∴|MN|的取值范围[$\frac{8\sqrt{2}}{3}$,6].
点评 本题重点考查极坐标和直角坐标的互化公式、距离问题处理思路和方法等知识,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | {a|a=kπ+$\frac{π}{2}$,k∈Z} | B. | {a|a=kπ,k∈Z} | ||
| C. | {a|a=2kπ+$\frac{π}{2}$,k∈Z} | D. | {a|a=kπ或a=kπ+$\frac{π}{2}$,k∈Z} |
| A. | (-∞,-1)∪(0,1) | B. | (0,1)∪(1,+∞) | C. | (-∞,-1)∪(-1,0) | D. | (-1,0)∪(1,+∞) |
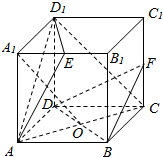 已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为A1B1中点,F为CC1中点,如图.
已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为A1B1中点,F为CC1中点,如图.