题目内容
20.已知集合P={a|a=$\frac{kπ}{2}$,k∈Z},则下列集合与集合P相等的是( )| A. | {a|a=kπ+$\frac{π}{2}$,k∈Z} | B. | {a|a=kπ,k∈Z} | ||
| C. | {a|a=2kπ+$\frac{π}{2}$,k∈Z} | D. | {a|a=kπ或a=kπ+$\frac{π}{2}$,k∈Z} |
分析 分析各个集合所表示的角的范围,可得答案.
解答 解:集合P={a|a=$\frac{kπ}{2}$,k∈Z}表示终边在坐标轴的角的集合;
集合{a|a=kπ+$\frac{π}{2}$,k∈Z}表示终边在y轴的角的集合;
集合{a|a=kπ,k∈Z}表示终边在x轴的角的集合;
集合{a|a=2kπ+$\frac{π}{2}$,k∈Z}表示终边在y轴非负半轴的角的集合;
集合{a|a=kπ或a=kπ+$\frac{π}{2}$,k∈Z}表示终边在坐标轴的角的集合;
故D答案中集合与P相等,
故选:D
点评 本题考查的知识点是集合的表示法,集合相等,正确理解各个集合表示的角的范围,是解答的关键.

练习册系列答案
相关题目
11.已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的底面边长为$\sqrt{6}$时,其高的值为( )
| A. | 3$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{3}$ |
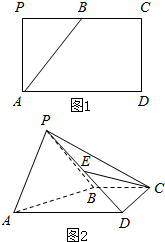 如图1,矩形APCD中,AD=2AP,B为PC的中点,将△APB折沿AB折起,使得PD=PC,如图2.
如图1,矩形APCD中,AD=2AP,B为PC的中点,将△APB折沿AB折起,使得PD=PC,如图2.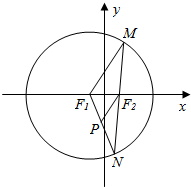 已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连结MF2并延长交圆F1于点N,连结F1N,过F2作F2P∥MF1交NF1于P,如图所示.
已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连结MF2并延长交圆F1于点N,连结F1N,过F2作F2P∥MF1交NF1于P,如图所示.