题目内容
9.已知函数f(x)=x2(x+a)-2(a∈R)在x=2处取得极值.(1)求实数a的值;
(2)求函数f(x)的单调区间,并指出其单调性;
(3)求函数f(x)在[-1,3]上的最大值.
分析 (Ⅰ)求出函数的导函数f′(x)=3x2+2ax,由x=2处取得极值解a.
(Ⅱ)利用导函数的符号,求出表达式的解集,即函数f(x)的单调递增区间,单调递减区间.
(Ⅲ)当x变化时,f′(x),f(x)的变化情况列表,求解函数的最值.
解答 (本小题满分13分)
解:(Ⅰ)由f(x)=x3+ax2-2得:f′(x)=3x2+2ax,…(2分)
依题意,得f′(2)=12+4a=0,…(3分)
解得:a=-3.…(4分)
(Ⅱ)由(Ⅰ)的结论知f′(x)=3x2-6x.
故由f′(x)=3x2-6x>0⇒x<0或x>2.…(6分)
由f′(x)=3x2-6x<0⇒0<x<2,…(8分)
即函数f(x)的单调递增区间为(-∞,0)和(2,+∞),单调递减区间为(0,2).…(9分)
(Ⅲ)当x变化时,f′(x),f(x)的变化情况如下表:
| x | -1 | (-1,0) | 0 | (0,2) | 2 | (2,3) | 3 |
| f′(x) | + | 0 | - | 0 | + | ||
| f(x) | -6 | 递增 | -2 | 递减 | -6 | 递增 | -2 |
由上表可知,当x=0或x=3时,函数取得最大值-2.…(13分)
点评 本题考查函数的对数的综合应用,函数的极值以及函数的单调性的应用,考查计算能力以及转化思想的应用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
18.已知等比数列{an}的各项均为正数,公比0<q<1,设P=$\frac{{a}_{3}+{a}_{9}}{2}$,Q=$\sqrt{{a}_{5}{a}_{7}}$,则a3,a9,P与Q的大小关系是( )
| A. | a3>P>Q>a9 | B. | a3>Q>P>a9 | C. | a9>P>a3>Q | D. | P>Q>a3>a9 |
19.下列说法正确的是( )
| A. | 命题“?x∈R使得x2+2x+3<0”的否定是:“?x∈R,x2+2x+3>0” | |
| B. | “p∧q为真命题”是“p∨q为真命题”的必要不充分条件 | |
| C. | “a>1”是“f(x)=logax(a>0,a≠1)在(0,+∞)上为增函数”的充要条件 | |
| D. | 命题p:“?x∈R,sinx+cosx≤$\sqrt{2}$”,则¬p是真命题 |
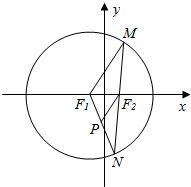 已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连结MF2并延长交圆F1于点N,连结F1N,过F2作F2P∥MF1交NF1于P,如图所示.
已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连结MF2并延长交圆F1于点N,连结F1N,过F2作F2P∥MF1交NF1于P,如图所示.