题目内容
13.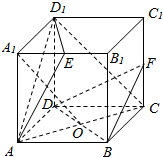 已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为A1B1中点,F为CC1中点,如图.
已知正方体ABCD-A1B1C1D1,底面ABCD的中心为O,E为A1B1中点,F为CC1中点,如图.(1)求证:A1O⊥BD;
(2)求证:A1O⊥平面BDF;
(3)求证:平面AD1E⊥平面ACD1.
分析 (1)利用线面垂直的判定定理证明DB⊥平面A1ACC1 ,证得A1O⊥DB.
(2)再用勾股定理证明A1O⊥OF,这样,A1O就垂直于平面GBD内的两条相交直线,故A1O⊥平面BDF.
(3)连接A1D交AD1于H,连接EH,B1D,证明B1D⊥平面ACD1,可得EH⊥平面ACD1,即可证明平面AD1E⊥平面ACD1.
解答  证明:(1)∵DB⊥A1A,DB⊥AC,A1A∩AC=A,
证明:(1)∵DB⊥A1A,DB⊥AC,A1A∩AC=A,
∴DB⊥平面A1ACC1.
又A1O?平面A1ACC1,∴A1O⊥DB;
(2)连接OF,则在矩形A1ACC1中,tan∠AA1O=$\frac{\sqrt{2}}{2}$,tan∠FOC=$\frac{\sqrt{2}}{2}$,
∴∠AA1O=∠GOC,
则∠A1OA+∠FOC=90°.∴A1O⊥OF.
∵OF∩DB=O,∴A1O⊥平面BDF;
(3)连接A1D交AD1于H,连接EH,B1D,则
∵E为A1B1中点,
∴EH∥B1D,
∵B1B⊥平面ABCD,AC⊥BD,
∴AC⊥B1D,
同理,AD1⊥B1D,
∵AD1∩AC=A,
∴B1D⊥平面ACD1,
∵EH∥B1D,
∴EH⊥平面ACD1,
∵EH?平面AD1E,
∴平面AD1E⊥平面ACD1.
点评 本题考查证明直线和平面垂直的方法,在其中一个平面内找出2条相交直线和另一个平面垂直是关键.

练习册系列答案
相关题目
11.已知正六棱柱的12个顶点都在一个半径为3的球面上,当正六棱柱的底面边长为$\sqrt{6}$时,其高的值为( )
| A. | 3$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{3}$ |
18.已知等比数列{an}的各项均为正数,公比0<q<1,设P=$\frac{{a}_{3}+{a}_{9}}{2}$,Q=$\sqrt{{a}_{5}{a}_{7}}$,则a3,a9,P与Q的大小关系是( )
| A. | a3>P>Q>a9 | B. | a3>Q>P>a9 | C. | a9>P>a3>Q | D. | P>Q>a3>a9 |
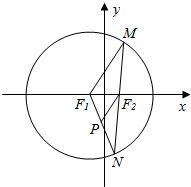 已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连结MF2并延长交圆F1于点N,连结F1N,过F2作F2P∥MF1交NF1于P,如图所示.
已知圆F1:(x+1)2+y2=16及点F2(1,0),在圆F1任取一点M,连结MF2并延长交圆F1于点N,连结F1N,过F2作F2P∥MF1交NF1于P,如图所示.