题目内容
 已知正三棱柱ABC-A′B′C′的正(主)视图和侧(左)视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,射线OA旋转所成的角为x弧度(x可以取到任意一个实数),对应的俯视图的面积为S(x),则函数S(x)的最大值为
已知正三棱柱ABC-A′B′C′的正(主)视图和侧(左)视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,射线OA旋转所成的角为x弧度(x可以取到任意一个实数),对应的俯视图的面积为S(x),则函数S(x)的最大值为8
8
;最小正周期为| π |
| 3 |
| π |
| 3 |
说明:“三棱柱绕直线OO′旋转”包括逆时针方向和顺时针方向,逆时针方向旋转时,OA旋转所成的角为正角,顺时针方向旋转时,OA旋转所成的角为负角.
分析:由题意判断俯视图的图形的形状,推出最大值时的位置,即可求解结果.
解答:解:由题意可知,正三棱柱的底面三角形的高为
,正三角形的边长为2,
俯视图是矩形,当此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图,底面正三角形的边在俯视图中为矩形的边长时,俯视图的面积最大,令俯视图的面积为S,则S的最大值为:2×4=8.
因为正三角形的内角均为60°,所以函数S(x)的最小正周期为
故答案为:8,
.
| 3 |
俯视图是矩形,当此三棱柱绕直线OO′旋转,在旋转过程中对应的俯视图,底面正三角形的边在俯视图中为矩形的边长时,俯视图的面积最大,令俯视图的面积为S,则S的最大值为:2×4=8.
因为正三角形的内角均为60°,所以函数S(x)的最小正周期为
| π |
| 3 |
故答案为:8,
| π |
| 3 |
点评:本题考查三视图与直观图的关系,解题的关键是判断俯视图的图形的形状,推出最大值时的位置.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
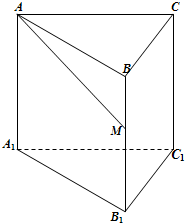 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ. 已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.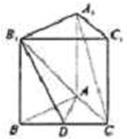 如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1. (2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.
(2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.