题目内容
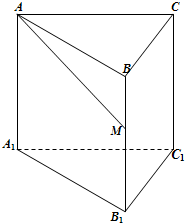如图，已知正三棱柱ABC-A1B1C1的底面边长为1，高为h（h＞2），动点M在侧棱BB1上移动．设AM与侧面BB1C1C所成的角为θ．（1）当θ∈[
| π |
| 6 |
| π |
| 4 |
（2）当θ=
| π |
| 6 |
| AM |
| BC |
分析：（1）先设BC的中点为D，连接AD，DM，根据题中条件
以及BB1⊥平面ABC得到AD⊥平面BB1CC1．进而得到∠AMD即为AM与侧面BCC1所成角θ；然后在Rt△ADM，利用角θ来求点M到平面ABC的距离的取值范围即可；
（2）先由第一问得BM=
；然后再把
转化为
+
，求出
•
即可表示出向量
与
夹角的大小．
|
（2）先由第一问得BM=
| 2 |
| AM |
| AB |
| BM |
| AM |
| BC |
| AM |
| BC |
解答：解：（1）设BC的中点为D，连接AD，DM，则有
?AD⊥BC ①
BB1⊥平面ABC?AD⊥BB1 ②
由①②得AD⊥平面BB1CC1．
于是，可知∠AMD即为AM与侧面BCC1所成角θ．
因为点M到平面ABC的距离为BM，设BM=x，x∈（0，h）．
在Rt△ADM中，tan∠AMD=
．
由AD=
，DM=
=
，
故tanθ=
．而当θ∈[
，
]时．tanθ∈[
，1]．
即
≤
≤1?3≤1+4x2≤9?
≤x2≤2．
所以，点M到平面ABC的距离BM的取值范围是：[
，
]．
（2）：当θ=
时，由第一问得BM=
．
故可得DM=
，AM=
=
．
设
与
的夹角为α．
因为
•
=（
+
）•
=
•
+
•
=1×1×cos120°+0=-
．
所以cosα=
=
=-
故向量
与
的夹角大小为：π-arccos
．
|
BB1⊥平面ABC?AD⊥BB1 ②
由①②得AD⊥平面BB1CC1．
于是，可知∠AMD即为AM与侧面BCC1所成角θ．
因为点M到平面ABC的距离为BM，设BM=x，x∈（0，h）．
在Rt△ADM中，tan∠AMD=
| AD |
| MD |
由AD=
| ||
| 2 |
| BD2+BM2 |
| ||
| 2 |
故tanθ=
| ||
|
| π |
| 6 |
| π |
| 4 |
| ||
| 3 |
即
| ||
| 3 |
| ||
|
| 1 |
| 2 |
所以，点M到平面ABC的距离BM的取值范围是：[
| ||
| 2 |
| 2 |
（2）：当θ=
| π |
| 6 |
| 2 |
故可得DM=
| 3 |
| 2 |
| AD2+DM2 |
| 3 |
设
| AM |
| BC |
因为
| AM |
| BC |
| AB |
| BM |
| BC |
| AB |
| BC |
| BM |
| BC |
=1×1×cos120°+0=-
| 1 |
| 2 |
所以cosα=
| ||||
|
|
-
| ||
|
| ||
| 6 |
故向量
| AM |
| BC |
| ||
| 6 |
点评：本题主要考查点到面的距离以及求两个向量的夹角问题．解决第2问的关键在于把
转化为
+
，再代入求出
•
的值，从而得到结论．
| AM |
| AB |
| BM |
| AM |
| BC |
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
相关题目
如图，已知正三棱柱ABC-A1B1C1各棱长都为a，P为线段A1B上的动点．
如图，已知正三棱柱ABC-A1B1C1的底面边长为2cm，高位5cm，一质点自A点出发，沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为
如图，已知正三棱柱ABC-A1B1C1的各条棱长都为a，P为A1B上的点．
如图，已知正三棱柱ABC-A1B1C1，D是AC的中点，
（2011•重庆三模）如图，已知正三棱柱ABC-A1B1C1的所有棱长均为a，截面AB1C和A1BC1相交于DE，则三棱锥B-B1DE的体积为