题目内容
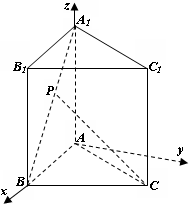
（2009•湖北模拟）如图，已知正三棱柱ABC-A1B1C1各棱长都为a，P为棱A1B上的动点．（Ⅰ）试确定A1P：PB的值，使得PC⊥AB；
（Ⅱ）若A1P：PB=2：3，求二面角P-AC-B的大小；
（Ⅲ）在（Ⅱ）的条件下，求点C1到面PAC的距离．
分析：（Ⅰ）以A为原点，AB为x轴，过A点与AB垂直的直线为y轴，AA1为z轴，建立空间直角坐标系A-xyz，利用
•
=0可求A1P：PB=1．
（Ⅱ）当A1P：PB=2：3时，求得P点的坐标是(
，0，
)．分别求出平面PAC、ABC的一个法向量．再用公式可求
（Ⅲ）设C1到面PAC的距离为d，利用d=
=
，可求．
| CP |
| AB |
（Ⅱ）当A1P：PB=2：3时，求得P点的坐标是(
| 2a |
| 5 |
| 3a |
| 5 |
（Ⅲ）设C1到面PAC的距离为d，利用d=
|
| ||||
|
|
| a |
| 2 |
解答：解：（Ⅰ）以A为原点，AB为x轴，过A点与AB垂直的直线为y轴，AA1为z轴，建立空间直角坐标系A-xyz，如图所示，
设P（x，0，z），则B（a，0，0）、A1（0，0，a）、C(
，
，0)．
（Ⅰ）由
•
=0得(x-
，-
，z)•(a，0，0)=0，
即(x-
)•a=0，∴x=
a，即P为A1B的中点，
也即A1P：PB=1时，PC⊥AB．…4′
（Ⅱ）当A1P：PB=2：3时，P点的坐标是(
，0，
)．取
=(3，-
，-2)．
则
•
=(3，-
，-2)•(
，0，
)=0，
•
=(3，-
，-2)•(
，
，0)=0．
∴
是平面PAC的一个法向量．
又平面ABC的一个法向量为
=(0，0，1)．
∴cos?
，
＞=
=
，∴二面角P-AC-B的大小是60°．…8′
（Ⅲ）设C1到面PAC的距离为d，则d=
=
，∴C1到面PAC的距离为
a．…12′
设P（x，0，z），则B（a，0，0）、A1（0，0，a）、C(
| a |
| 2 |
| ||
| 2 |
（Ⅰ）由
| CP |
| AB |
| a |
| 2 |
| ||
| 2 |
即(x-
| a |
| 2 |
| 1 |
| 2 |
也即A1P：PB=1时，PC⊥AB．…4′
（Ⅱ）当A1P：PB=2：3时，P点的坐标是(
| 2a |
| 5 |
| 3a |
| 5 |
| m |
| 3 |
则
| m |
| AP |
| 3 |
| 2a |
| 5 |
| 3a |
| 5 |
| m |
| AC |
| 3 |
| a |
| 2 |
| ||
| 2 |
∴
| m |
又平面ABC的一个法向量为
| n |
∴cos?
| m |
| n |
| ||||
|
|
| 1 |
| 2 |
（Ⅲ）设C1到面PAC的距离为d，则d=
|
| ||||
|
|
| a |
| 2 |
| 1 |
| 2 |
点评：本题以正三棱柱为载体，考查空间向量的运用，考查线线位置关系，考查二面角，考查点到面距离．
练习册系列答案
相关题目